第五章约束优化方法VIP免费

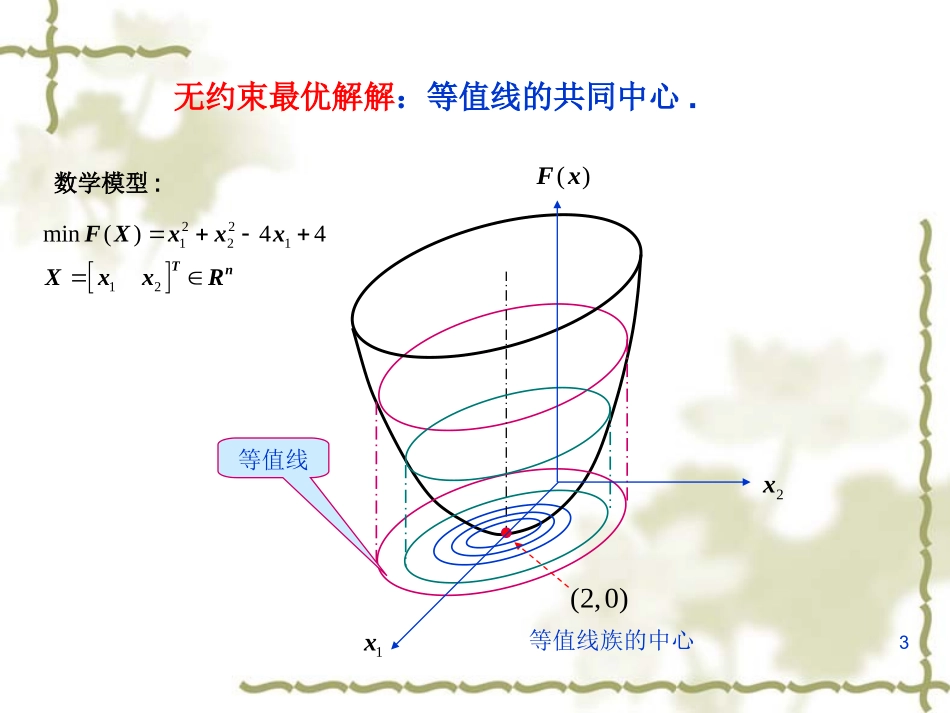
1第五章第五章约束优化方法约束优化方法5.1约束优化问题的最优解5.2约束优化问题极小点的条件5.3常用的约束优化方法5.3.1约束坐标轮换法5.3.2约束随机方向法5.3.3复合形法5.3.5惩罚函数法2概述约束优化问题最优解****12...TnXxxx*min()()FXFX最优值最优点约束最优解和无约束最优解无论是在数学模型上还是几何意义上均是不同的概念3(2,0)等值线等值线族的中心1x()Fx2x无约束最优解解：等值线的共同中心.2212112min()44TnFXxxxXxxR数学模型:4数学模型:1x()Fx2x可行域约束最优解51x2xo211()gX4()gX3()gX2()gX*1X*120TX无约束最优点*2X*20.581.34TX约束最优点6约束优化问题的类型1.不等式约束优化问题(IP型)2.等式约束优化问题(EP型)3.一般约束优化问题(GP型)7约束优化方法分类约束优化方法约束优化方法约束约束坐标轮换法坐标轮换法直接法：直接法：约束随机方向法约束随机方向法复合形法复合形法间接法：间接法：惩罚函数法惩罚函数法直接法：设法使每一次迭代产生的新迭代点限制在可行域内，且一步一步的降低目标函数值，直至最后获得一个可行域内的约束最优解。间接法：将约束优化问题通过一定形式的变换，转化为无约束优化问题，然后采用约束优化方法进行求解。85.3.1约束坐标轮换法基本思想:与无约束坐标轮换法类似,依此沿坐标轴方向寻优,逐步逼近最优点。1x2xo(0)X(1)1X(1)2X(1)3X(1)4X(1)X(2)1X(2)1X(2)2X(2)3X(2)X(3)X(4)X91x2xo(0)X(1)1X(1)2X(1)3X(1)4X(1)X任取一个初始点(0)XD取初始步长α0沿e1方向(1)(0)11XXe0检查可行性:适用性:(1)(0)1?FXFX(1)1?XD2(1)(0)21XXe检查......加速步长(1)(0)31,2XXe(1)(0)41,2XXe检查可行性:适用性:(1)1)?(XD(1)(1)3XX101x2xo(0)X(1)1X(1)2X(1)3X(1)4X(1)X(2)1X(2)1X(2)2X(2)3X(2)X沿e2方向(2)(1)12XXe0检查可行性:适用性:(2)(1)1?FXFX(2)1?XD(2)(0)22,2XXe检查可行性:适用性:(2)2?XD(2)(2)2XX检查可行性:适用性:(2)(1)1()?FXFX(1)2?XD(2)(1)12XXe(2)(1)2?FXFX(2)(0)32,2XXe检查可行性:适用性:(2)3)?(XD111x2xo(0)X(1)1X(1)2X(1)3X(1)4X(1)X(2)1X(2)1X(2)2X(2)3X(2)X(3)X沿e1方向(3)(2)11XXe0检查可行性:适用性:(3)2)?(XD2(4)(0)12XXe检查可行性:适用性:(3)(2)1?FXFX(3)1?XD(3)(2)21XXe(3)(3)1XX沿e2方向0检查可行性:适用性:(4)(3)1()?FXFX(4)1?XD0(4)(0)12XXe检查......121x2xo(0)X(1)1X(1)2X(1)3X(1)4X(1)X(2)1X(2)1X(2)2X(2)3X(2)X(3)X沿坐标轴方向找不到合适的点:缩减初始步长α0←0.5α0继续迭代终止准则:α0≤ε约束坐标轮换法与无约束坐标轮换法的区别：①步长无约束:最优步长约束:加速步长②对每一个迭代点的检查无约束:检查适用性约束:检查适用性和可行性③终止准则无约束:点距准则约束:步长准则13特点:1x2xo(0)X(1)1X(1)2X(1)3X(1)4X(1)X(2)1X(2)1X(2)2X(2)3X(2)X(3)X约束坐标轮换法具有算法明了、迭代简单、便于设计者掌握运用等优点。但是，它的收敛速度较慢，对于维数较高的优化问题(例如10维以上)很费机时。另外，这种方法在某些情况下还会出现“死点”的病态，导致输出伪最优点。避免输出伪最优点的办法:1、输入不同的初始点2、用不同的不长多次计算14基本原理：典型的“瞎子爬山”式的数值选代解法。在可行域内，任选初始点x(0)，以给定的步长a=a0，沿按某方法产生的随机方向S(1)取探索点x=x(0)+aS(1），若该点同时符合下降性（F(x)