第五章 线性系统的频率分析法VIP免费

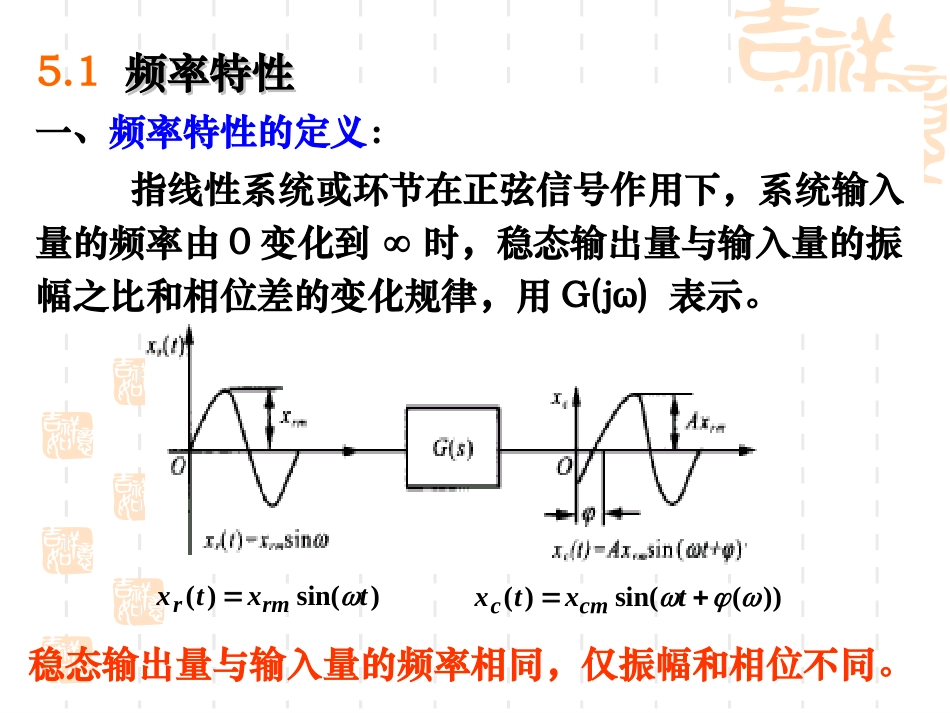
第五章线性系统的频域分析法第五章线性系统的频域分析法本章主要内容本章主要内容::5.I5.I5.25.25.35.35.45.4频率特性频率特性控制系统开环频率特性控制系统开环频率特性频率域稳定判据频率域稳定判据稳定裕度稳定裕度一、频率特性的定义：指线性系统或环节在正弦信号作用下，系统输入量的频率由0变化到时，稳态输出量与输入量的振幅之比和相位差的变化规律，用G(jω)表示。5.1频率特性频率特性稳态输出量与输入量的频率相同，仅振幅和相位不同。)sin()(txtxrmr))(sin()(txtxcmc)j(G)(A)j(G)(幅频特性：稳态输出与输入振幅之比，即：相频特性：稳态输出与输入相位之差，即：G(jω)：包含了幅频特性和相频特性，故称其为幅相频率特性表达式。)j(G)j(G)j(R)j(C)j(G频率特性)R(j)C(j)G(j三、频率特性的求取根据定义求取：jsG(s))G(j根据传递函数求取：1）极坐标形式：)()(jeA)G(j2）直角坐标形式：)j(jImG)j(ReG)j(G3）两种坐标间转换：)(I)(Re)G(j)(A2m2jGjG)(ReG)(ImGtg)(1-jj二、频率特性的表示形式例如：求右图的频率特性微分方程：传递函数：令s=jω代入传递函数得频率特性：ioouudtduRC1Ts11RCs1(s)U(s)UG(s)io1jT1jG)(iuRouC频率特性是传递函数的特例，是定义在复平面虚轴上的传递函数，因此频率特性与系统的微分方程、传递函数一样反映了系统的固有特性。系统传递函数微分方程频率特性jsdtdsjdtd微分方程、传递函数、频率特性之间的关系：四、频率特性的几何表示法频率特性的几何表示法常用频率特性的三种表示法：1)幅相频率特性曲线（又称：幅相曲线、奈奎斯特图（NyquistNyquist））、极坐标图）2)对数频率特性曲线（又称：伯德图(Bode)）频率对数分度,幅值/相角线性分度3)对数幅相曲线（又称：尼科尔斯曲线、Nichols）以频率为参变量表示对数幅值和相角关系：L(ω)—(ω)图请重点掌握前面两种！1、幅相频率特性曲线（又叫奈奎斯特图）手工绘制：以横轴为实轴，纵轴为虚轴，构成复平面，取几个特殊值时的幅值和相角，然后根据G(jω)随ω值的变化的趋势画出幅相曲线的大概形状。注：1）参变量ω在复平面上并不出现，只用箭头表示ω增大时幅相曲线的变化方向。2）通常只画ω从0到∞的幅相曲线，而ω从0到-∞的幅相曲线与前者关于实轴对称。实轴正方向相角零度线，逆时针正角度，顺时针负角度例如：的（幅相曲线）奈氏图：1Ts1sG)(Ttg1T11Tj1jG122)(2）取三个特殊点：90-0)G(j01G(j0)4521T1jGj0011）频率特性：3）画出幅相曲线：1）对数频率特性曲线的横坐标：标记ω，按lgω对数分度，单位是弧度/秒（rad/s）；2）对数幅频特性曲线的纵坐标：以L(ω)=20lgA(ω)线性分度，单位是分贝（dB）；3）对数相频特性曲线的纵坐标：按φ(ω)线性分度，单位是度（o）。2、对数频率特性曲线（又叫伯德图Bode）包含：对数幅频特性和对数相频特性两条曲线1801100.1204060-20-40-60090180902346857)(dBL)(对数幅频特性对数相频特性十倍频程dec对数分度：当变量每增大或减小10倍（10倍频程），坐标距离变化一个单位长度十倍频程dec1）横轴按ω的对数lgω标尺分度，但标出的是ω本身的数值，即刻度不均匀；2）横轴压缩了高频段，扩展了低频段；3）在ω轴上，十倍频程的长度相等；4）可以将幅值的乘除化为加减L(ω)=20lgA(ω)；5）满足直线方程：斜率k对数频率特性曲线的特点：1212lglgLLk)()(例如：的（对数频率特性曲线）伯德图1Ts1sG)(Ttg1T11Tj1jG122)(2）对数频率特性：1）频率特性：3）画出伯德图：1T1201gL22)(Ttg1)(-40-30-20-100Magnitude(dB)10-1100101102-90-450Phase(deg)BodeDiagramFrequency(rad/sec)最小相位环节和非最小相位环节的区别：最小相位环节：K>0,开环零极点在s左半平面；非最小相位环节：K<0开环零极点在s右半平面；s-2222e1s2s1Ts2sT11s1Ts1ss1K...