固定收益证券第五章VIP免费

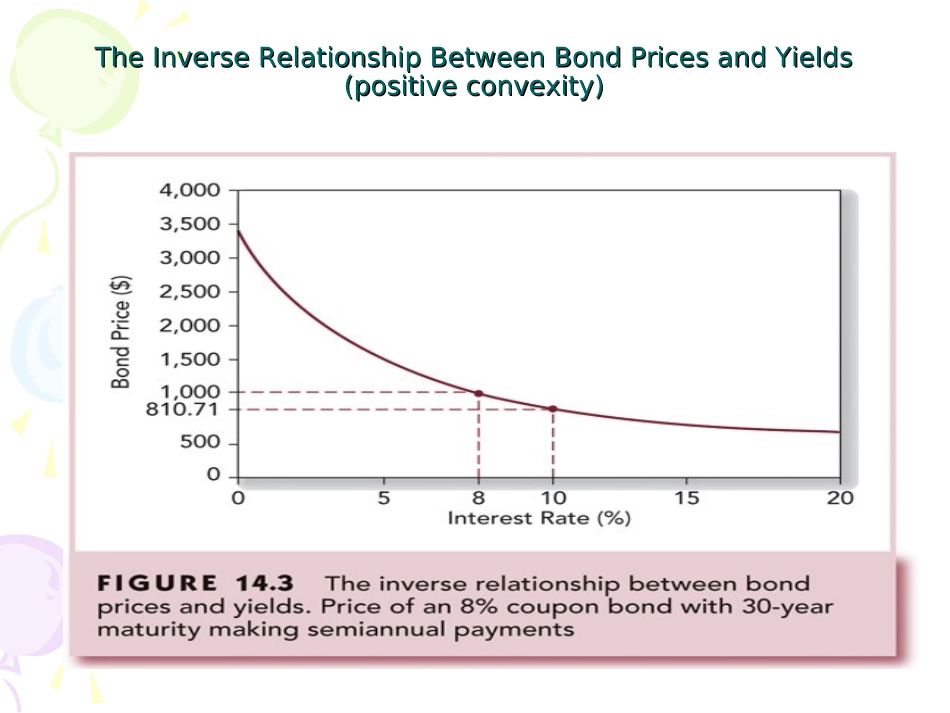
第第55讲债券的利率风讲债券的利率风险险1.债券价格与市场收益率之间的关系2.债券利率风险的度量----久期3.影响久期的因素4.债券的凸度1.债券价格与市场收益率之间的关系特征1)债券价格与收益率呈反向变动关系2)债券收益率变化引起的价格变化具有不对称性由收益率上升引起的价格下降幅度低于收益率的同等下降引起的价格上升的幅度。凸状convex3)期权影响债券的凸度TheInverseRelationshipBetweenBondPricesandYieldsTheInverseRelationshipBetweenBondPricesandYields(positiveconvexity)(positiveconvexity)Figure14.4BondPrices:CallableandFigure14.4BondPrices:CallableandStraightDebtStraightDebt2.2.债券利率风险的度量债券利率风险的度量--------久期久期债券利率风险：债券价格的利率敏感性完全定价分析法市场利率波动对价格的影响（10年期债券）期限现金流初始利率变化幅度（基点）6.0050.00100.00-50.00-100.0013533.9833.9033.8234.0634.1523532.9932.8332.6733.1533.3133532.0331.8031.5732.2632.5043531.1030.8030.5031.4031.7153530.1929.8329.4730.5630.9363529.3128.8928.4729.7430.1873528.4627.9827.5128.9529.4483527.6327.1026.5828.1728.7393526.8226.2525.6827.4228.03103526.0425.4224.8126.6827.34113525.2824.6223.9725.9726.68123524.5523.8423.1625.2726.02133523.8323.0922.3824.6025.39143523.1422.3721.6223.9424.77153522.4721.6620.8923.3024.17163521.8120.9820.1822.6823.58173521.1820.3219.5022.0723.00183520.5619.6818.8421.4822.44193519.9619.0618.2120.9021.89201035573.05545.93520.16601.59631.63债券价值1,074.391,036.351,000.001,114.201,155.89债券价格变化幅度0-3.54%-6.92%3.71%7.59%久期-凸度分析法债券价格的利率敏感性与泰勒展开泰勒展开222111......2!!nnnVdVdVdVdydydyVtVtdyVtdynVtdy2.1久期收益率变动1%而导致的债券价格的百分比变化价格的百分比变动与收益率变动的比率（一阶敏感性）dVVtDdy美元久期：$D单位利率变动引起的证券价值变动金额dytdVtVD久期的含义数学含义：价格利率函数的一阶导数经济含义：由于一阶导数捕捉了债券价值的利率敏感性中的主要部分，因此久期和美元久期反映了债券利率风险的主要部分。久期与美元久期的绝对值越大，固定收益证券的利率风险越大；反之则越小。几何含义：久期反映债券价格收益率曲线上各点的切线斜率2.2有效久期考虑到债券价格-收益率曲线的凸性和债券定价的复杂性收益率同幅度的上升和下降带来的平均价格波动适用于内含期权的债券，其现金流可能因利率变动而改变久期计算的核心在于一阶导的计算•简单的证券：直接求导•复杂的证券：有效久期（effectiveduration）2.3麦考利久期Macaulay’sdurationAmeasureoftheeffectivematurityofabond债券的每次利息和本金现金流支付时间的加权平均，权重则是每一时点的现金流的现值占债券价格的比例。适用于不含权债券icePryCwttt)1(twtDTt1tperiodforFlowCashCtY=10%Y=10%Spreadsheet16.1CalculatingtheSpreadsheet16.1CalculatingtheM.DurationofTwoBondsM.DurationofTwoBonds零息票债券的M久期就等于它的到期期限，而息票债券的M久期比它的到期期限短。将P看作是1+y的函数，可以有对于1+y的微小变化，有111(1)(1)1TttttCdPPDdyyy(1)1PyDPy定义：修正久期D*=D/(1+y)，且Δ(1+y)=Δy，债券价格变化的百分比等于修正久期与收益率变化的乘积。*PDyP2.4修正久期麦考利久期的特点：经济含义直观，可以视为付息期限的一种加权平均，单位是年，相应地修正久期的单位也是年，这是久期名称的最初来源。修正久期才是真正的利率风险度量指标；麦考利久期是计算公式中的一部分若收益率以连续复利计算，不存在麦考利久期和修正久期的差别。二者的计算依赖于定价模型久期与期限加权之间并没有必然联系，其单位也并不必然为年麦考利久期、修正久期、有效久期的比较前二者不考虑收益率变动对未来现金流的影响有效久期...