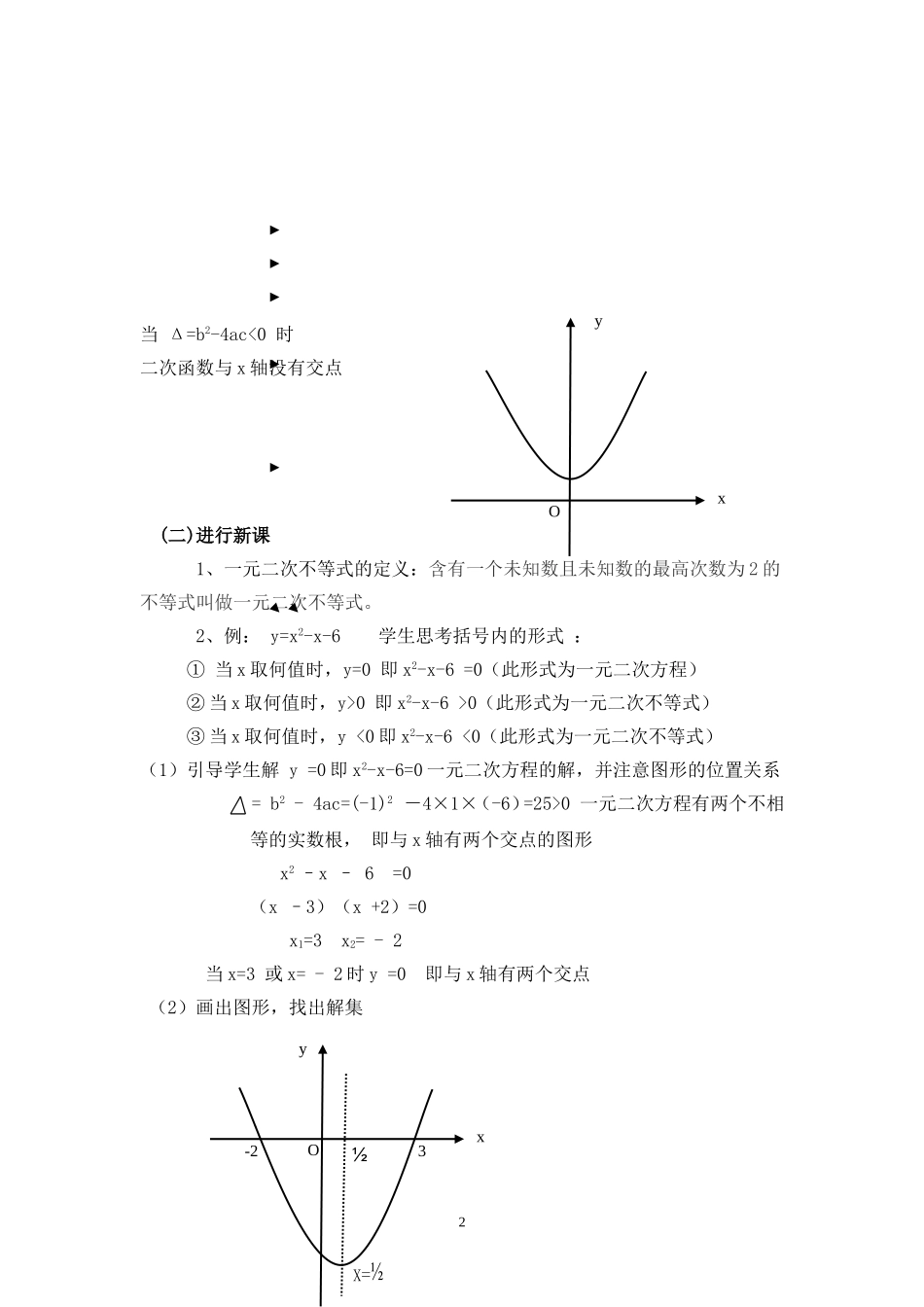
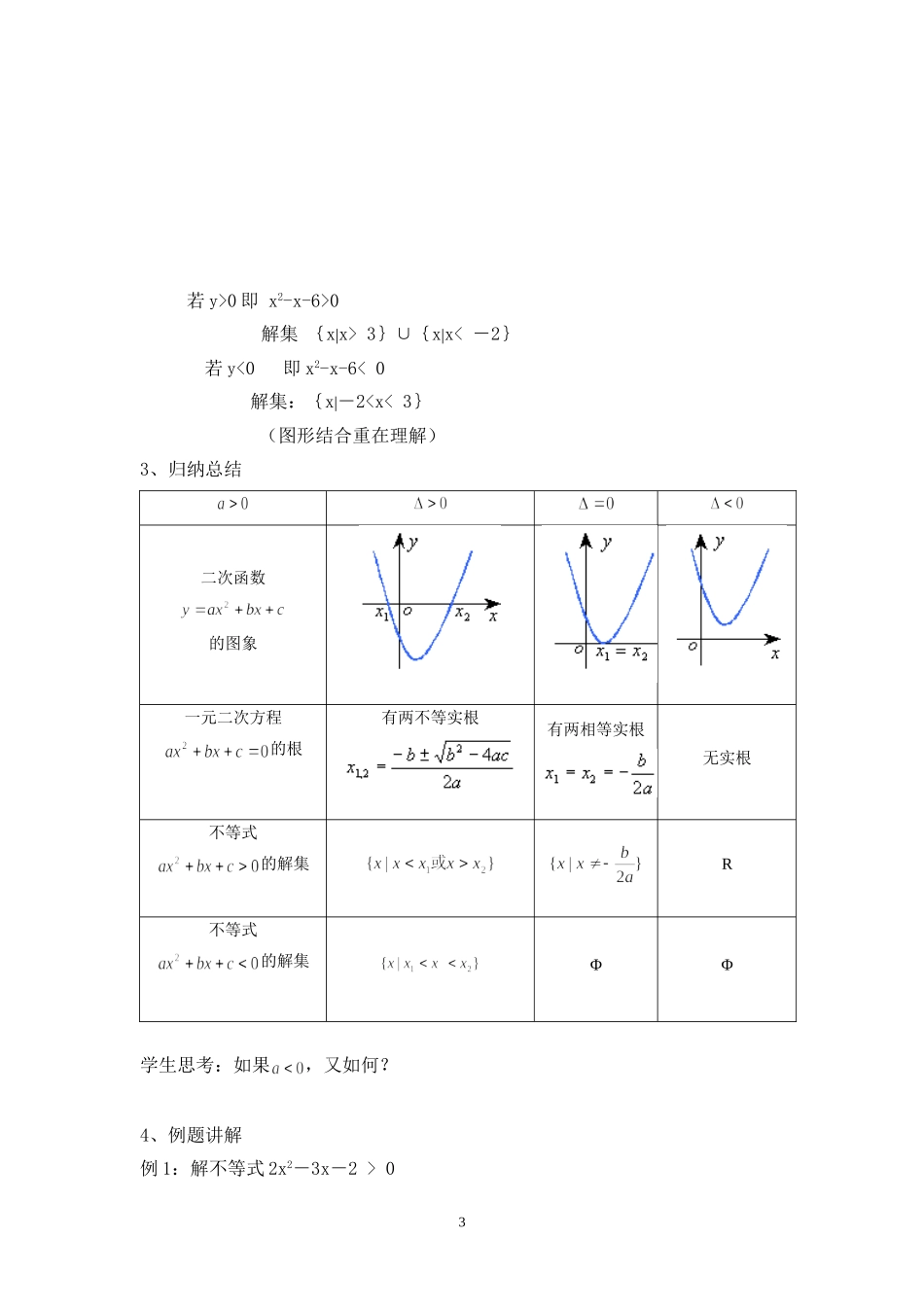
一元二次不等式及其解法一、教学目标(一)知识与技能1、知道一元二次不等式的概念2、会利用图像求一元二次不等式的解集(二)能力目标培养数形结合的能力,培养分类讨论的思想方法,培养抽象概括能力和逻辑思维能力;(三)情感、态度、价值观激发学习数学的热情,培养勇于探索的精神,勇于创新精神,同时体会事物之间普遍联系的辩证思想。二、教学重点与难点(一)重点1、会求一元二次不等式的解集2、会利用图像表示一元二次不等式的解集(二)难点会求一元二次不等式的解集三、教学方法图形结合,讲练结合四、教学过程设计(一)导入巩固二次函数图像画法。假设a>0,b=0,则当Δ=b2-4ac>0时二次函数与x轴有两个交点x1,x2当Δ=b2-4ac=0时二次函数与x轴有一个交点x01x2x1Oxyx0Oxy当Δ=b2-4ac<0时二次函数与x轴没有交点(二)进行新课1、一元二次不等式的定义:含有一个未知数且未知数的最高次数为2的不等式叫做一元二次不等式。2、例:y=x2-x-6学生思考括号内的形式:①当x取何值时,y=0即x2-x-6=0(此形式为一元二次方程)②当x取何值时,y>0即x2-x-6>0(此形式为一元二次不等式)③当x取何值时,y<0即x2-x-6<0(此形式为一元二次不等式)(1)引导学生解y=0即x2-x-6=0一元二次方程的解,并注意图形的位置关系=b2-4ac=(-1)2-4×1×(-6)=25>0一元二次方程有两个不相等的实数根,即与x轴有两个交点的图形x2–x–6=0(x–3)(x+2)=0x1=3x2=-2当x=3或x=-2时y=0即与x轴有两个交点(2)画出图形,找出解集2Oxy½X=½y-23Ox若y>0即x2-x-6>0解集{x|x>3}∪{x|x<-2}若y<0即x2-x-6<0解集:{x|-203解:化为2x2-3x-2=0求解x1=-x2=2画草图原不等式2x2-3x-2>0的解集{x|x1<-}∪{x|x2>2}例2:解不等式-x2+2x-3>0解:将原不等式变形得:x2-2x+3<0∵Δ<0,对应方程x2-2x+3=0无实数解∴不等式x2-2x+3<0解集是ø故原不等式的解集是ø。学生总结解题步骤:(1)二项系数化正(2)判断的值(求根)(3)画出草图(4)写出解集5、课堂练习:(1)、(2)、五、作业4x-½X=¾y2¾O