13四种命题VIP免费

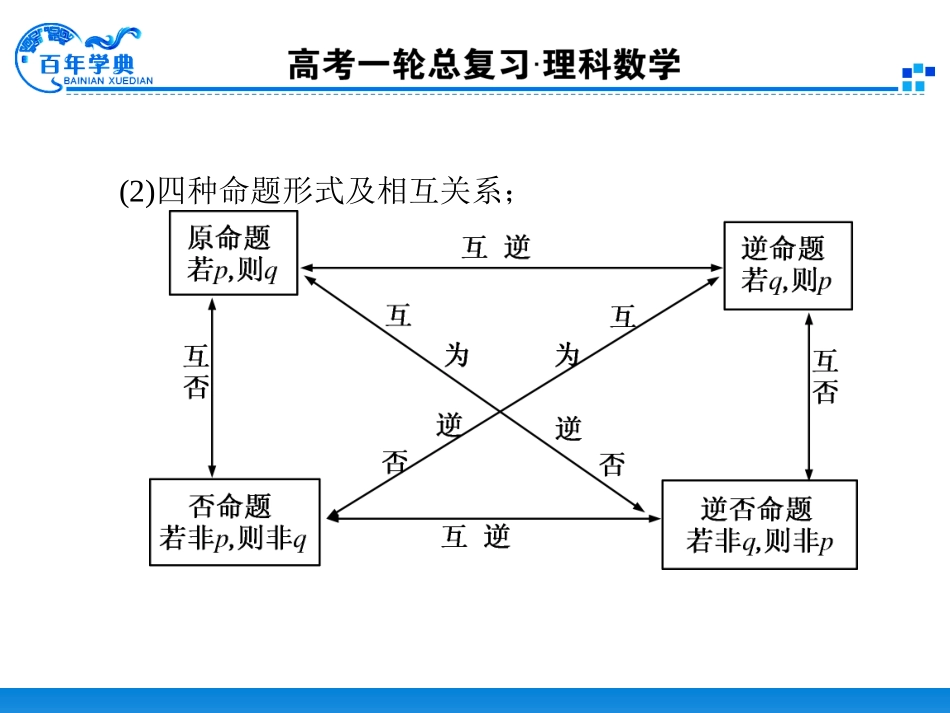
1．命题及其关系(1)命题：用____________________表达，可以判定________的陈述句．常见基本结构：____________；形式：__________；分类：真命题，假命题．语言、符号或式子真假条件＋结论若p，则q(2)四种命题形式及相互关系；(3)四种命题的真假性之间的关系：两个命题互为逆否命题，它们有______的真假性；两个命题互为逆命题或互为否命题，它们的真假性______关系．相同没有2．充分条件与必要条件(1)充分条件、必要条件和充要条件的含义：充分条件：若p⇒q，则p是q的____________；必要条件：若q⇒p，则p是q的____________；充要条件：若p⇒q，且q⇒p，则p是q的____________，即p⇔q；p是q的充分不必要条件：____________；p是q的必要不充分条件：____________；p是q的既不充分又不必要条件：p⇒/q且q⇒/p.注意：如果甲是乙的充分条件，则乙是甲的必要条件；反之亦然．充分条件必要条件充要条件p⇒q且qpq⇒p且pq(2)从集合的角度理解充分条件、必要条件和充要条件：记条件p，q对应的集合分别为P，Q，一般有：若P⊆Q，则p是q的___________________；若Q⊆P，则p是q的___________________；若PQ，则p是q的___________________；若QP，则p是q的___________________；若P＝Q，则p是q的___________________．充分条件必要条件充分不必要条件必要不充分条件充要条件题型一判断命题及其真假下列四个命题中真命题的个数为()①若两平面有三个公共点，则这两个平面重合；②两条直线可以确定一个平面；③若M∈α，M∈β，α∩β＝l，则M∈l；④空间中，相交于同一点的三条直线在同一平面内．A．1B．2C．3D．4【思路分析】根据命题本身涉及的知识去判断真假，判断一个命题为真，一般要进行严格的逻辑推理，但判断一个命题为假，只要举出一个反例即可．【答案】A【解析】①是假命题，两平面也可能相交；②是假命题，若两直线是异面直线，不可能确定一个平面；④是假命题，两相交直线确定一个平面，第三条直线过该交点，可与该平面相交．故选A.【点拨】数学中的定义、公理、定理都是命题.但命题与定理是有区别的，命题有真假之分，而定理都是真命题.陈述句“在2016年，巴西将举办第31届夏季奥林匹克运动会”是命题吗？【解析】是命题，在2016年，巴西将举办第31届夏季奥林匹克运动会，是真是假，虽然目前还无法确定，但是随着时间推移，总能确定它的真假，所以我们把这类猜想仍算为命题．题型二写出一个命题的逆命题、否命题、逆否命题写出下述命题的逆命题、否命题、逆否命题．(1)若x2＋y2＝0，则x，y全为0；(2)若a＋b是偶数，则a，b都是偶数；(3)若x＝3或x＝7，则(x－3)(x－7)＝0.【思路分析】“都”的否定词是“不都”，而不是“都不”，同理“全”的否定词是“不全”，而不是“全不”．另外，原命题中的“或”，在否命题中要改为“且”．要认真体会它们的区别．【解析】因为原命题是“若p，则q”的形式，根据其他三种命题的构造方法，分别写出其逆命题、否命题、逆否命题．(1)逆命题：若x，y全为0，则x2＋y2＝0.否命题：若x2＋y2≠0，则x，y不全为0.逆否命题：若x，y不全为0，则x2＋y2≠0.(2)逆命题：若a，b都是偶数，则a＋b是偶数．否命题：若a＋b不是偶数，则a，b不都是偶数．逆否命题：若a，b不都是偶数，则a＋b不是偶数．(3)逆命题：若(x－3)(x－7)＝0，则x＝3或x＝7.否命题：若x≠3且x≠7，则(x－3)(x－7)≠0.逆否命题：若(x－3)(x－7)≠0，则x≠3且x≠7.【点拨】认清命题的条件p和结论q，然后按定义写出逆命题、否命题、逆否命题即可.命题“若m＞0，则m＋1m≥2”的逆命题是_________．【答案】“若m＋1m≥2，则m>0”．题型三判断充分与必要条件指出下列命题中，p是q的什么条件(在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分也不必要条件”中选出一种作答)．(1)在△ABC中，p：∠A＝∠B，q：sinA＝sinB；(2)对于实数x，y，p：x＋y≠8，q：x≠2或y≠6；(3)非空集合A，B中，p：x∈A∪B，q：x∈B；(4)已知x，y∈R，p：(x－1)2＋(y－2)2＝0，q：(x－1)(y－2)＝0.【思路分析】有三种基本判断方法：直接由条件看能否推出结论；利用逆否命题的真假；画图表...