课件.3-实数(1)VIP免费

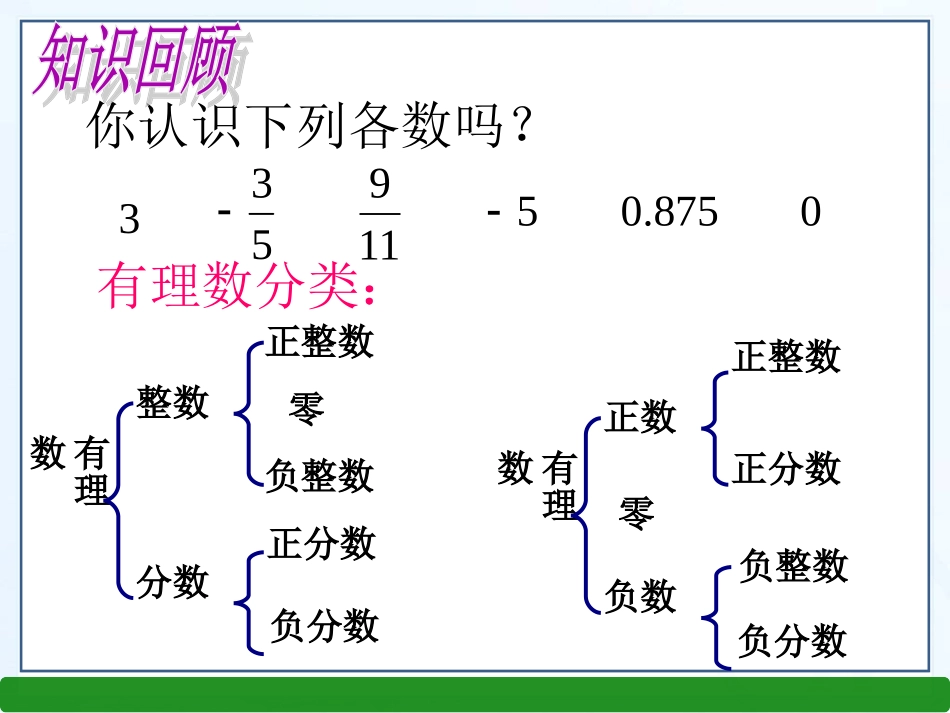
义务教育教科书（RJ）七年级数学下册第六章实数你认识下列各数吗？有理数分类：353875.011905有理数整数分数正整数零负整数正分数负分数有理数正数负数正整数零负整数正分数负分数把下列各数写成小数的形式：整数和分数统称为有理数353847119911950.36.0875.518.021.05.0有限小数无限循环小数有限小数和无限循环小数叫有理数使用计算器，把下列有理数化成小数的形式：=3.0=-0.6任何一个有理数都能写成有限小数或无限循环小数的形式反过来任何有限小数或无限循环小数也都是有理数；35-9115930.81～～0.5～～2探究一、无理数把下列各数写成小数的形式：353335374142.17320.12360.2442.1710.1913.1无限不循环小数14159265.3无限不循环小数叫无理数无理数：无限不循环小数有理数：有限小数或无限循环小数实数探究二、实数的分类：1.按定义分分数整数女孩子男孩子妈妈开方开不尽的数有规律但不循环的数含有的数～负实数正实数数实正有理数负有理数2.按性质分O正无理数负无理数性格开朗的大孩子性格内向的小孩子0正实数负实数探究三、范例把下列各数分别填入相应的集合内：1,432,7,,5,22,20,35,38,4,90,0.3737737773（相邻两个3之间的7的个数逐次加1）有理数集合无理数集合38,1,45,24,90,32,7,,2,20,35,0.3737737773做一做：1.把下列各数分别填在相应的集合中。有理数集合无理数集合0-80.63.14159263—√3—√36227—√70.191191119…每相邻两个9之间依次多一个12.2.判断快枪手判断快枪手————看谁最快最准！看谁最快最准！1.实数不是有理数就是无理数。（）2.无理数都是无限不循环小数。（）4.无理数都是无限小数。（）3.带根号的数都是无理数。（）5.无理数一定都带根号。（）××探究四、在数轴上表示下列各数：-3-2-10123403126.3031203126.3有理数都可以用数轴上的点表示那么无理数是否也可以用数轴上的点来表示呢？如果可以你能在数轴上找到表示这样的无理数的点吗？2、直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上的一点由原点到达O′，点O′的坐标是多少？01234O′探究四、01234你有什么发现？无理数π可以用数轴上的点表示O′再探以单位长度为边长画一个正方形，以原点为圆心，正方形对角线为半径画弧，与正半轴的交点表示什么？-2-1012222无理数可以用数轴上的点表示2每一个有理数都可以用数轴上的点表示；每一个无理数都可以用数轴上的点表示；数轴上的点有些表示有理数，有些表示无理数。每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。在数轴上的两个点，右边的点表示的实数总比左边的点表示的实数大。归纳：实数与数轴上点的关系6.3实数(1)1无理数：无限不循环小数。2无理数的常见形式：（1）开方开不尽的数；（2）圆周率，以及一些含有的数；（3）有规律但不循环的无限小数4实数的分类：二分法和三分法。5实数与数轴的关系：一一对应。01234O′1、下列各数，，，，，中，有理数的个数有()A2个B3个C4个D5个712)3(14.3202、在，，，，中，无理数分别是。31338001001000100.0039C393001001000100.03.判断题无理数是无限小数,无限小数就是无理数。无理数包括正无理数,0,负无理数.带根号的数都是无理数,不带根号的数都是有理数。×××4.是一个分数.22×5.把下列各数填入相应的集合内：935646.043039313.0（1）有理数集合{（2）无理数集合{（3）整数集合{（4）负数集合{（5）分数集合{（6）实数集合{3539433996439646.043313.06.04313.0935646.04339313.0｝｝｝｝｝｝