大学物理第四章习题解答VIP免费

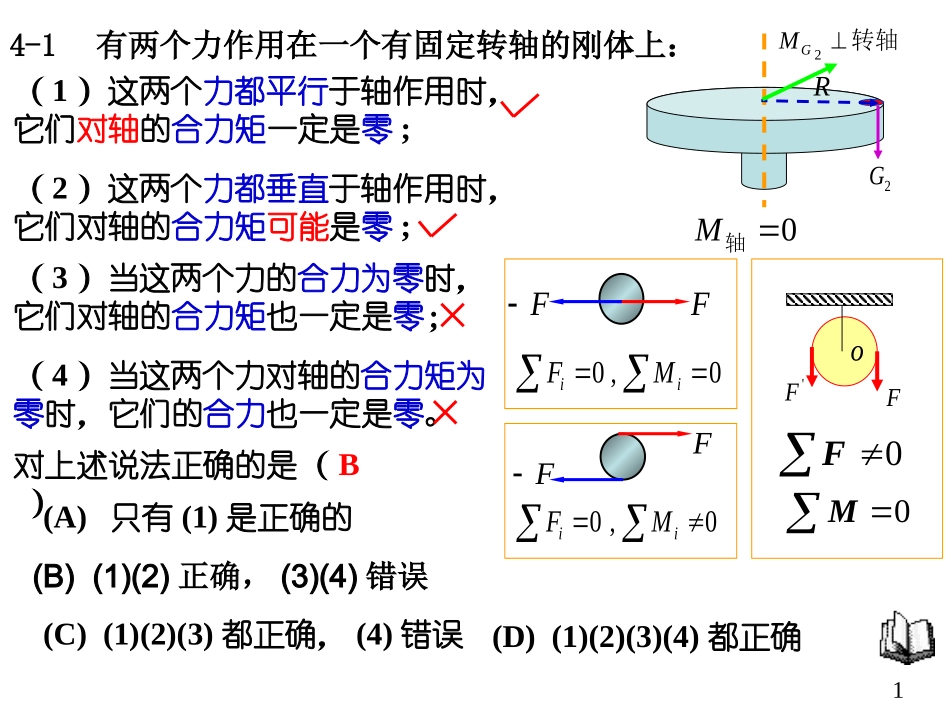
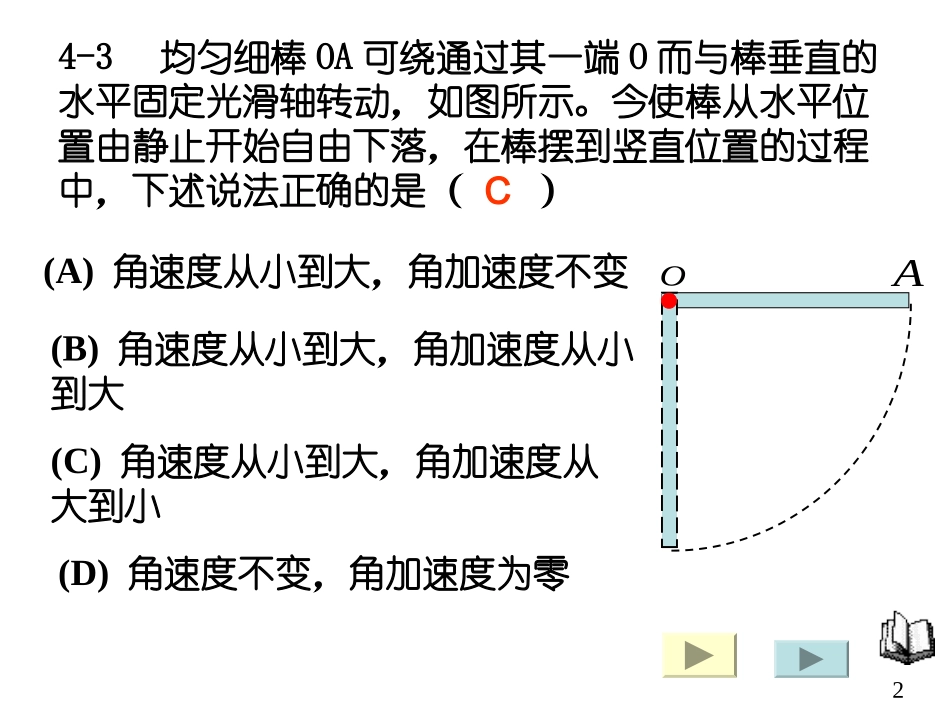
14-1有两个力作用在一个有固定转轴的刚体上：（1）这两个力都平行于轴作用时，它们对轴的合力矩一定是零;（2）这两个力都垂直于轴作用时，它们对轴的合力矩可能是零;（3）当这两个力的合力为零时，它们对轴的合力矩也一定是零；对上述说法正确的是（）(A)只有(1)是正确的(C)(1)(2)(3)都正确，(4)错误B（4）当这两个力对轴的合力矩为零时，它们的合力也一定是零。(D)(1)(2)(3)(4)都正确(B)(1)(2)正确，(3)(4)错误2GR转轴2GM0轴M0,0iiMFFF0,0iiMFFFo'FF0M0F24-3均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动，如图所示。今使棒从水平位置由静止开始自由下落，在棒摆到竖直位置的过程中，下述说法正确的是（）(A)角速度从小到大，角加速度不变(B)角速度从小到大，角加速度从小到大(C)角速度从小到大，角加速度从大到小(D)角速度不变，角加速度为零OAC3OA绕过O点的轴做定轴转动。求：运动过程中角速度和角加速度的变化情况受力和运动分析:gmrgmJM刚体定轴转动定律：sinsinrmgrFM090:M2122212121JJMd因棒由静止开始下摆，与转向一致，所以角速度由小变大。另：另：机械能守恒44-5假设卫星环绕地球中心作椭圆运动，则在运动过程中，卫星对地球中心的（）(A)角动量守恒，动能守恒(B)角动量守恒，机械能守恒(C)角动量不守恒，机械能守恒(D)角动量不守恒，动量也不守恒(E)角动量守恒，动量也守恒Bh2mh1引力矢量和过地心,对地心力矩为零以卫星和地球为系统，忽略其它外界作用，系统的机械能守恒。5内转过的圈数。）启动后变化的规律；（）角加速度随时间时的转速；（）。求：（，，式中随时间变化的关系为某种电动机启动后转速sstssradet632612/91:7400解：6dtedtt60/060)1()]()(-[tdedt/t6060060][/tet0)]e-([602629/edte/t6001)(rad.936)(87.52圈NN7对轴的转动惯量。，求飞轮飞轮的密度为的共轴圆柱体组成，设，长为的圆盘和两个直径都为，厚度为：一飞轮由一直径为33/108.781023094mkgcmcmcmcm解：柱盘JJJ2221盘盘盘RmJ221柱柱柱RmJmR210302盘mR210102柱盘盘Vm柱柱Vm2136.0mkgJ8）绳的张力。距离；（后的由静止开始下降）物体，求：（的物体端系一个质量为其一的柔绳绕在圆柱体上，阻力忽略不计。一条轻绕其固定水平轴转动，，可以，其半径为的实心圆柱体如图所示，质量21181516:13421sBBkgmcmrAkgmrABgm21T2TTTTraamTgmrmJrTBA2121221221：（运动方向为正方向），列出方程如下和解：分别研究2222122212121rmTrgrmrmTrrmTgmrmTr9加速度和绳的张力。的略去不计。试求两物体略去不计，绳的质量也绳索与轮间的摩擦力均，轮与轴承间、和为，两轮的转动惯量分别和设两轮的半径分别为组合轮两端。分别悬挂在如图所示的、的两物体和质量为2121:144JJrRBAmmrABgm11TF1TFRgm22TF2TF解:受力分析2a1aPNF运动分析1111amFgmT2222amgmFT)(2121JJrFRFTTRa1ra210grrmRmJJrmRmragRrmRmJJrmRmRarmRmJJgrmgRm222121212222121211222121211111amFgmT2222amgmFT)(2121JJrFRFTTRa1ra2gmrmRmJJrRmRmJJFgmrmRmJJRrmrmJJFTT2222121121212122212122221111的角速度。到弹陷入杆中，试求所得向与杆及轴正交。若子的速度射入杆端，其方的子弹，以的轴转动，一质量为通过其中点并与之垂直，可绕，长木杆，其质量在光滑的水平面上有一smvgmcmlkgm/20010401:21421sradlmlmvmJJJ/13.2936212212解：子弹+杆系统：0外M)J(J212Jrv2/lv211121lmJ212)2(lmJ12分析：蜘蛛与转台系统：（蜘蛛无初速度落在...