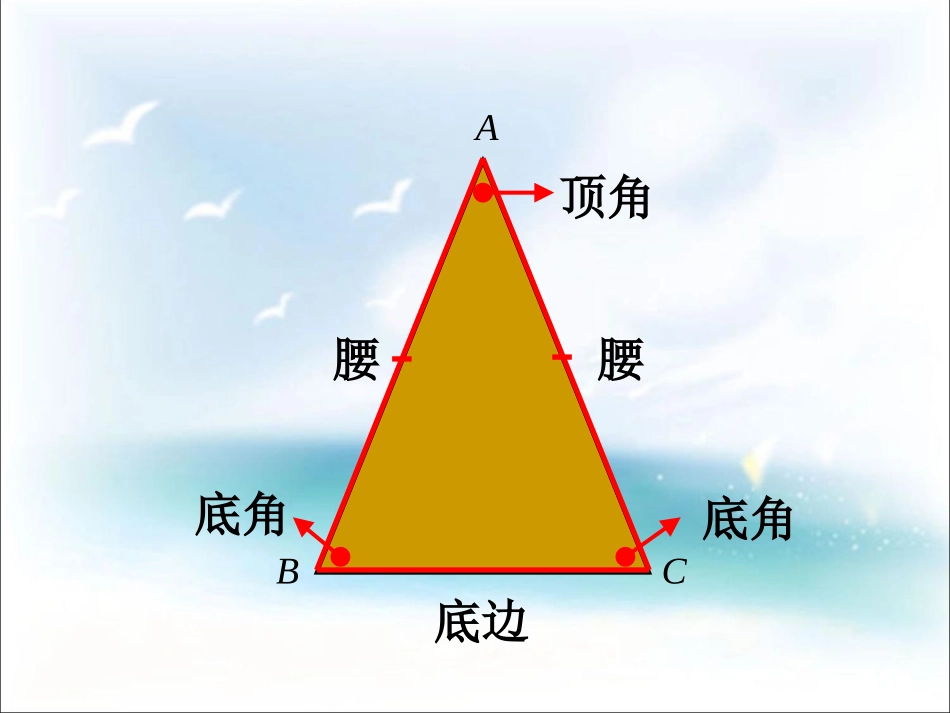
10.2等腰三角形复习什么样的三角形叫做等腰三角形?(有两边相等的三角形)ABC腰顶角底边底角腰底角(1)把你们准备的顶角分别为锐角、直角和钝角的等腰三角形拿出来.(2)把三角形的顶角顶点记为A,底角顶点记为B,C.(3)把三角形对折,让两腰AB,AC重叠在一起,折痕为AD.观察后你发现了什么现象?BACDABCD1.等腰三角形是轴对称图形2.∠B=∠C3.BD=CD,AD为底边上的中线4.∠ADB=∠ADC=90°,AD为底边上的高5.∠BAD=∠CAD,AD为顶角平分线问题1、结论(2)用文字如何表述?等腰三角形的两个底角相等(简写“等边对等角”)问题2、结论(3)、(4)、(5)用一句话可以归纳为什么?CABD性质定理:性质定理:等腰三角形的两个底角相等(简写成“等边对等角”).几何书写: AB=AC(已知)∴B=C(等边对角)CAB∴AD⊥BCBD=CD(等腰三角形三线合一)几何书写: AB=AC(已知)∠1=2∠(已知)推论:等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合.(三线合一)DCAB12证明:作顶角的平分线AD.在△BAD和△CAD中,AB=AC(已知),∠1=2∠(辅助线作法),AD=AD(公共边),∴△BAD≌△CAD(SAS).∴∠B=∠C(全等三角形的对应角相等).已知:△ABC中,AB=AC.求证:∠B=∠C.ABC12证明:等腰三角形的两个底角相等作顶角的平分线D证明等腰三角形的性质证明:作底边中线AD.在△BAD和△CAD中,AB=AC(已知),BD=CD(辅助线作法),AD=AD(公共边),∴△BAD≌△CAD(SSS).∴∠B=∠C(全等三角形的对应角相等).已知:△ABC中,AB=AC.求证:∠B=∠C.ABCD证明:等腰三角形的两个底角相等作底边中线证明等腰三角形的性质证明:作底边高线AD.AB=AC(已知),AD=AD(公共边),∴Rt△BADRt≌△CAD(HL).∴∠B=∠C(全等三角形的对应角相等).已知:△ABC中,AB=AC.求证:∠B=∠C.ABCD证明:等腰三角形的两个底角相等作底边的高线在Rt△BAD和△RtCAD中,证明等腰三角形的性质已知:如图,在△ABC中,AB=AC,BD、CE是△ABC的角平分线.例1.证明:等腰三角形两底角的平分线相等.用心想一想,马到功成21EDCBA求证:BD=CE.证明: AB=AC,∴∠ABC=∠ACB(等边对等角). ∠1=∠ABC,∠2=∠ACB,∴∠1=2∠.在△BDC和△CEB中, ∠ACB=∠ABC,BC=CB,∠1=2∠.∴△BDC≌△CEB(ASA).∴BD=CE(全等三角形的对应边相等).12121、已知:在△ABC中,AB=AC,∠A=80。求∠C和∠B的度数.ACB练习2、已知△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.ABCD解: AB=AC,(已知)∴∠ABC=∠C(等边对等角) BD=BC=AD,(已知)∴∠C=∠BDC(等边对等角)∠A=∠ABD设∠A=x°,则∠ABD=x°,∠BDC=2x°,∠C=2x°,x°x°2x°2x°根据题意得:x+2x+2x=180x=36即∠A=36°∠ABC=∠ACB=72°练习3、已知AD⊥BC,试找出等腰三角形ABC(AB=AC)中,存在相等关系的量.CBDA12∠B=∠C∠1=2∠∠BDA=∠CDA=90°BD=CD练习4、填空:在△ABC中,AB=AC,D在BC上,(1)如果AD⊥BC,那么∠BAD=______∠,BD=______.(2)如果∠BAD=∠CAD,那么AD⊥___,BD=___.(3)如果BD=CD,那么∠BAD=_____∠,AD⊥___,∠ADB=_____=___°∠ABCDCADCDBCCDCADBCADCADC9090练习5、在三角形ABC中,AB=AC,且AD⊥BC,已知BD=2cm,求DC=___cm,BC=___cm?CBDA12 AB=AC,AD⊥BC(已知)∴BD=CD(等腰三角形的高与底边上的中线重合)即(等腰三角形三线合一) BD=2cm(已知)∴CD=2cm练习通过本节课的学习,你有哪些收获?定理:等边对等角推论:“三线合一”常用来证明两角相等,求等腰三角形各角的度数.研究等腰三角形的有关问题时“三线”是常用的辅助线.等腰三角形建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道其中反映了什么数学原理?问题已知△ABC中,∠A=60°,().请你在括号内补充一个条件,使△ABC能成为等边三角形.∠B=60°(或∠C=60°)AB=BC、AC=BC、AB=BC=AC创设情境,导入新知ABC思考2这个特殊的直角三角形相比一般的直角三角形有什么不同之处,它有什么特殊性质?创设情境,导入新知思考1等边三角形是轴对称图形,若沿着其中一条对称轴折叠,能产生什么特殊图形?活动用两个全等的含30°角的直角三角尺...