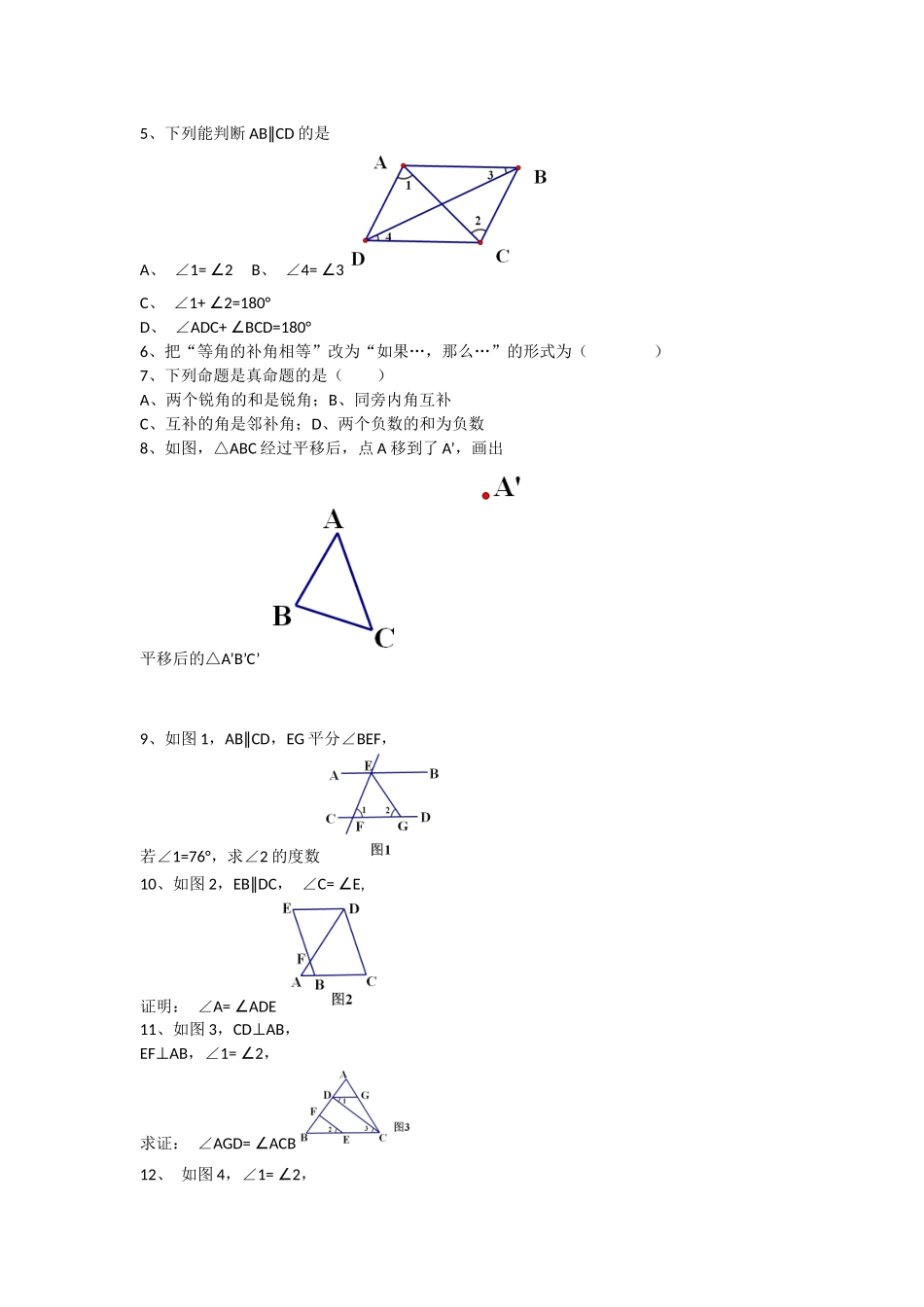
一、知识要点回顾(一)相交线1、邻补角的和为()°;2、对顶角()3、过一点()条直线与已知直线垂直4、连接直线外一点与直线上各点的所有线段中,()最短,简单说成:()(二)平行线5、经过直线外一点,()条直线与这条直线平行6、平行线的判定、性质7、如果两条直线都与第三条直线平行,那么这两条直线()8、垂直于同一条直线的两条直线()(三)命题9、什么是命题?10、命题由哪两部分组成?11、命题可以分为哪两种?(四)平移12、平移时,新图形与原图形的()和()完全相同;连接各对应点的线段()且()二、典型例题1、下列图形中,∠1和∠2是对顶角的是()2、如右图,若∠AOC=30°,则∠BOD=()°,BOC=∠()°3、如图,OHAB⊥,OA=OB=5cm,OH=3cm,P在AB上,则OP的取值范围是()4、经过两次转弯后,行走的方向相同,则可能是()A、第一次左转100°,第二次左转100°B、第一次左转100°,第二次左转80°C、第一次左转100°,第二次右转100°D、第一次左转100°,第二次右转80°5、下列能判断ABCD∥的是A、∠1=2B∠、∠4=3∠C、∠1+2=180°∠D、∠ADC+BCD=180°∠6、把“等角的补角相等”改为“如果…,那么…”的形式为()7、下列命题是真命题的是()A、两个锐角的和是锐角;B、同旁内角互补C、互补的角是邻补角;D、两个负数的和为负数8、如图,△ABC经过平移后,点A移到了A’,画出平移后的△A’B’C’9、如图1,ABCD∥,EG平分∠BEF,若∠1=76°,求∠2的度数10、如图2,EBDC∥,∠C=E,∠证明:∠A=ADE∠11、如图3,CDAB⊥,EFAB⊥,∠1=2∠,求证:∠AGD=ACB∠12、如图4,∠1=2∠,C=D,∠∠求证:∠A=F∠13、如图5,∠D=E,∠ABE=D+E,∠∠∠BC是∠ABE的平分线,求证:BCDE∥14、如图,已知ABCD∥,请猜想各个图中∠AMC与∠MAB、∠MCD的关系三.本节课结束,谢谢!再见!