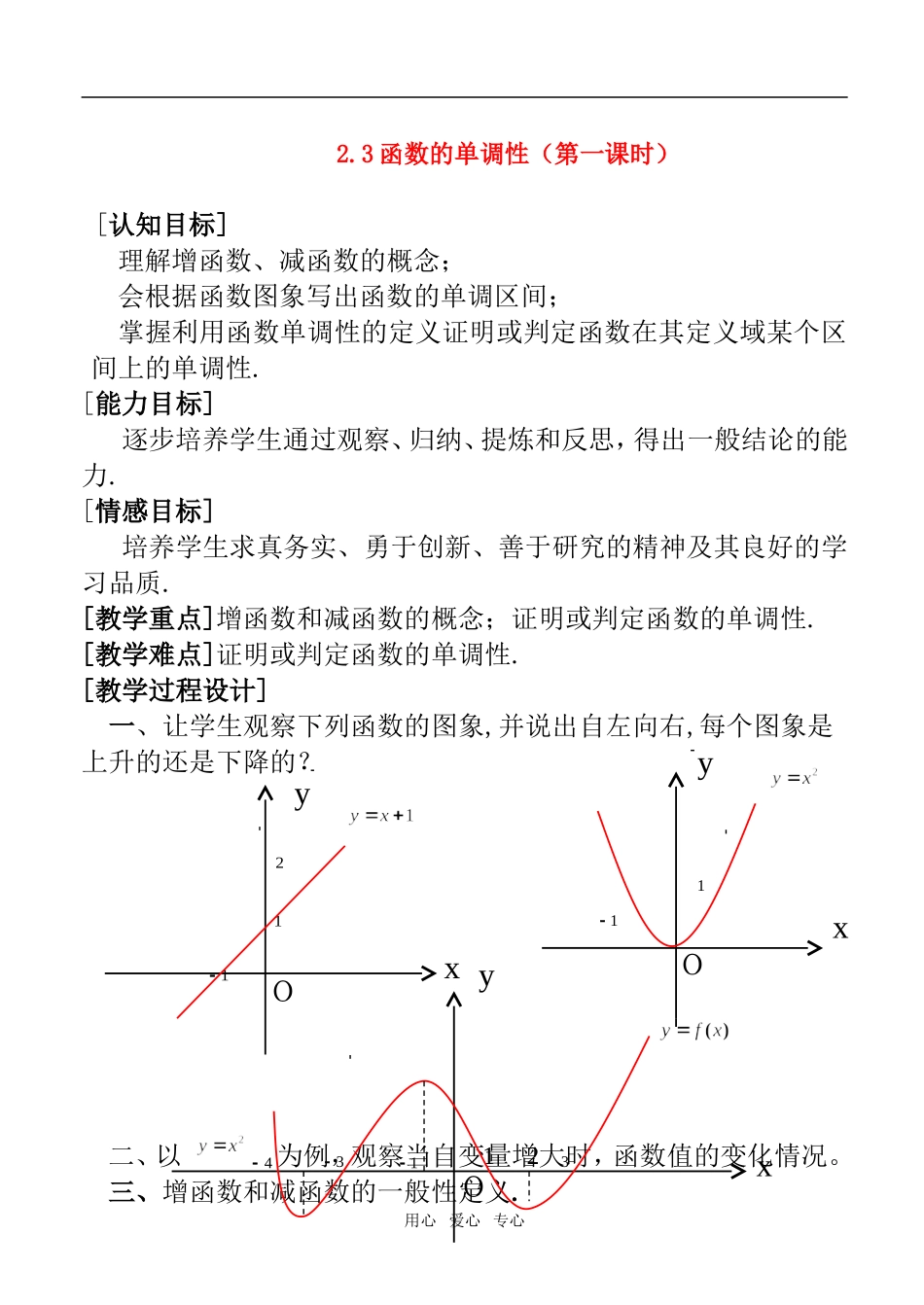
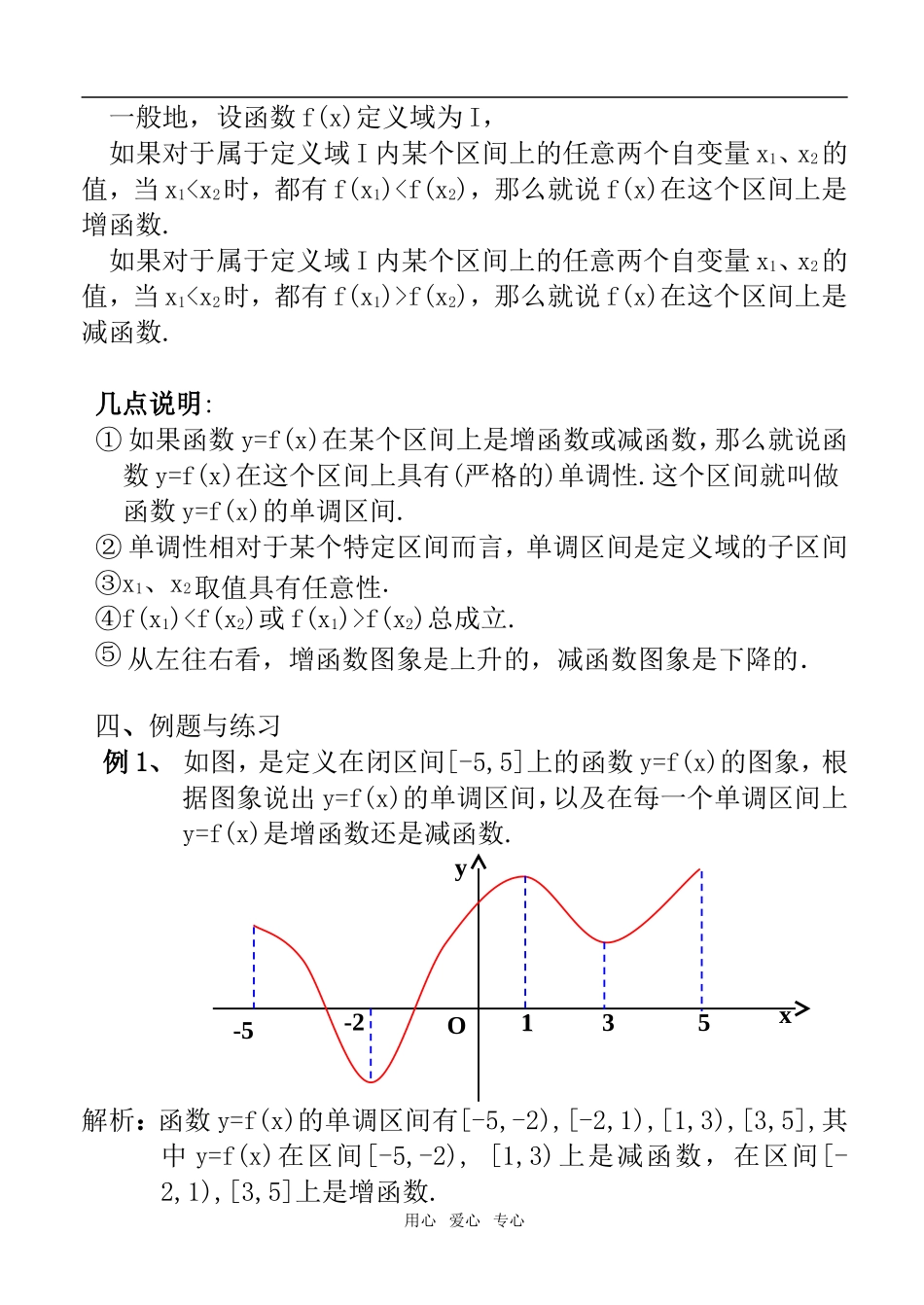
2.3函数的单调性(第一课时)[认知目标]理解增函数、减函数的概念;会根据函数图象写出函数的单调区间;掌握利用函数单调性的定义证明或判定函数在其定义域某个区间上的单调性.[能力目标]逐步培养学生通过观察、归纳、提炼和反思,得出一般结论的能力.[情感目标]培养学生求真务实、勇于创新、善于研究的精神及其良好的学习品质.[教学重点]增函数和减函数的概念;证明或判定函数的单调性.[教学难点]证明或判定函数的单调性.[教学过程设计]一、让学生观察下列函数的图象,并说出自左向右,每个图象是上升的还是下降的?二、以为例,观察当自变量增大时,函数值的变化情况。三、增函数和减函数的一般性定义.用心爱心专心11yxOx21yO3134xy21O1一般地,设函数f(x)定义域为I,如果对于属于定义域I内某个区间上的任意两个自变量x1、x2的值,当x1f(x2),那么就说f(x)在这个区间上是减函数.几点说明:①如果函数y=f(x)在某个区间上是增函数或减函数,那么就说函数y=f(x)在这个区间上具有(严格的)单调性.这个区间就叫做函数y=f(x)的单调区间.②单调性相对于某个特定区间而言,单调区间是定义域的子区间③x1、x2取值具有任意性.④f(x1)f(x2)总成立.⑤从左往右看,增函数图象是上升的,减函数图象是下降的.四、例题与练习例1、如图,是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上y=f(x)是增函数还是减函数.解析:函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中y=f(x)在区间[-5,-2),[1,3)上是减函数,在区间[-2,1),[3,5]上是增函数.用心爱心专心-5-2O35xy11练习:判断下列函数的单调性:(1)函数f(x)=-3x+2在(-∞,+∞)上是;(2)函数f(x)=-x2在(0,+∞)上是;(3)函数f(x)=1x在(-∞,0)上是.例2、证明函数f(x)=3x+2在R上是增函数.证明:设x1,x2是R上的任意两个实数,x1