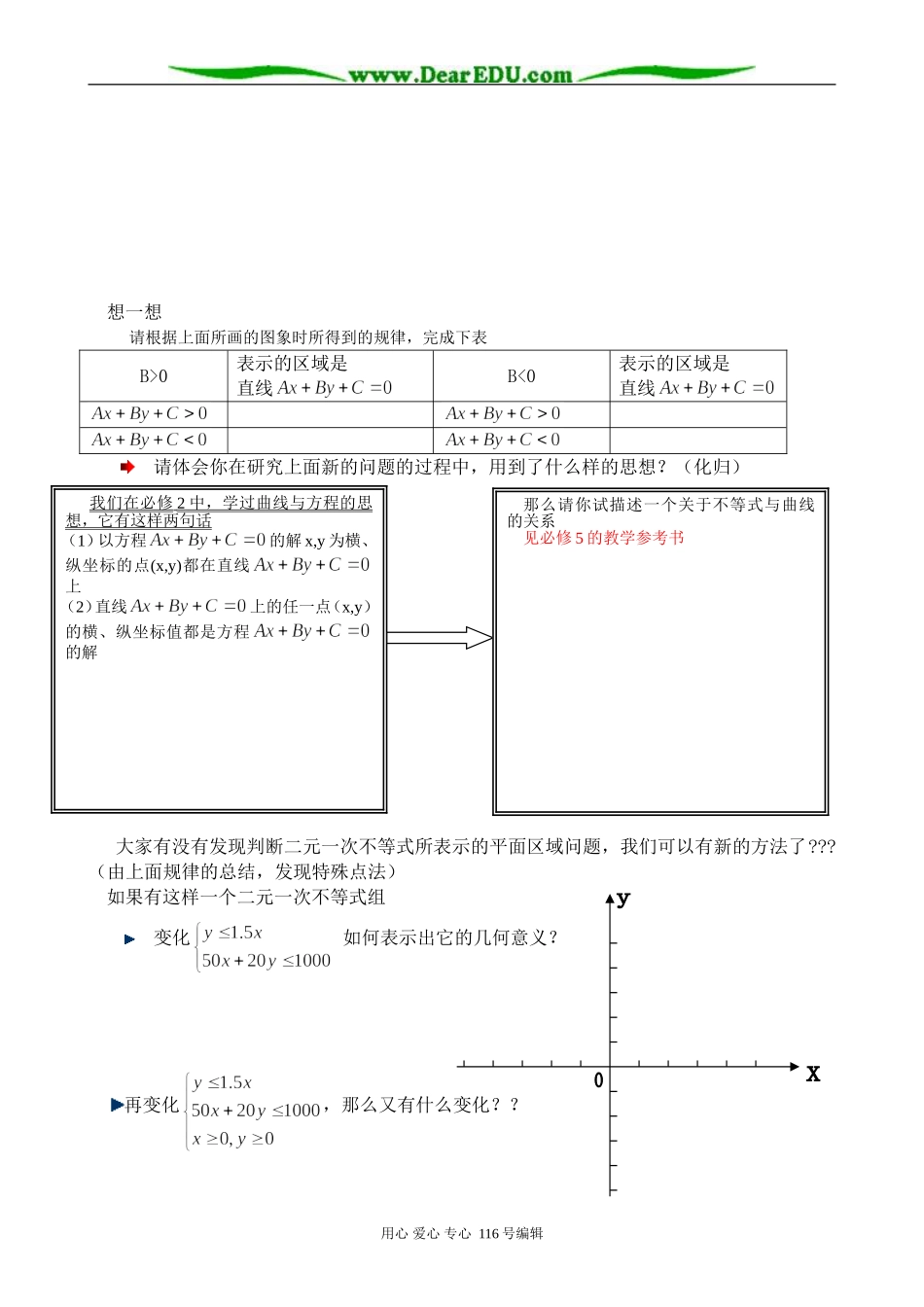
实际问题数学模型数学模型的解实际问题的解二元一次不等式(组)所表示的平面区域【教学目标】1.知识与技能:了解二元一次不等式的几何意义,会用二元一次不等式组表示平面区域;2.过程与方法:经历从实际情境中抽象出二元一次不等式组的过程,提高数学建模的能力;3.情态与价值:通过本节课的学习,体会数学来源与生活,提高数学学习兴趣。【教学重点】用二元一次不等式(组)表示平面区域;【教学过程】Jack准备在2006年德国世界杯期间,一边看球,一边去卖点纪念品。现在他有本钱1000美元,准备投入去购买单价50美元球衣和单价20元足球纪念品,希望使足球纪念品,球衣的总数尽可能多,但足球纪念品数量不多于球衣数量1.5倍,那么Jack买足球纪念品和球衣各多少才行?一般实际问题的求解步骤如下表:你有遇到什么难题了吗?设:球衣x件,足球纪念品y只,总和为SS=x+y学生此时应该到第三步,无法解决数学模型的解!二元一次不等式所表示的平面区域对于像上面这样有两个参量控制的取值范围问题,我们都可以用下面的几何方法来求解。第一步:研究出问题的约束条件,确定数对(x,y)的范围第二步:在第一步所得到的数对(x,y)的范围中,通过图形的方法,找出所求问题达到最大数对的(x,y)我们不妨来画出其中一个练一练(1)(2)(3)(4)用心爱心专心116号编辑小结:一般地,直线y=kx+b把平面分成两个部分:__________________________________________________________想一想请根据上面所画的图象时所得到的规律,完成下表B>0表示的区域是直线B<0表示的区域是直线请体会你在研究上面新的问题的过程中,用到了什么样的思想?(化归)大家有没有发现判断二元一次不等式所表示的平面区域问题,我们可以有新的方法了???(由上面规律的总结,发现特殊点法)如果有这样一个二元一次不等式组变化如何表示出它的几何意义?再变化,那么又有什么变化??用心爱心专心116号编辑我们在必修2中,学过曲线与方程的思想,它有这样两句话(1)以方程的解x,y为横、纵坐标的点(x,y)都在直线上(2)直线上的任一点(x,y)的横、纵坐标值都是方程的解那么请你试描述一个关于不等式与曲线的关系见必修5的教学参考书再再变化那么又有什么变化???如果问题现在倒过来怎么办呢?倒过来:如果给出阴影,如何用不等式表示!小结:我们今天学习了:________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________作业:书P78页练习4,580页1,2,3,4!并阅读P88页上的第7题的阅读题,并写下你的感受!用心爱心专心116号编辑