高中数学 第三章 指数函数和对数函数 3.4.1 对数的概念教学设计3 北师大版必修1-北师大版高一必修1数学教案VIP免费

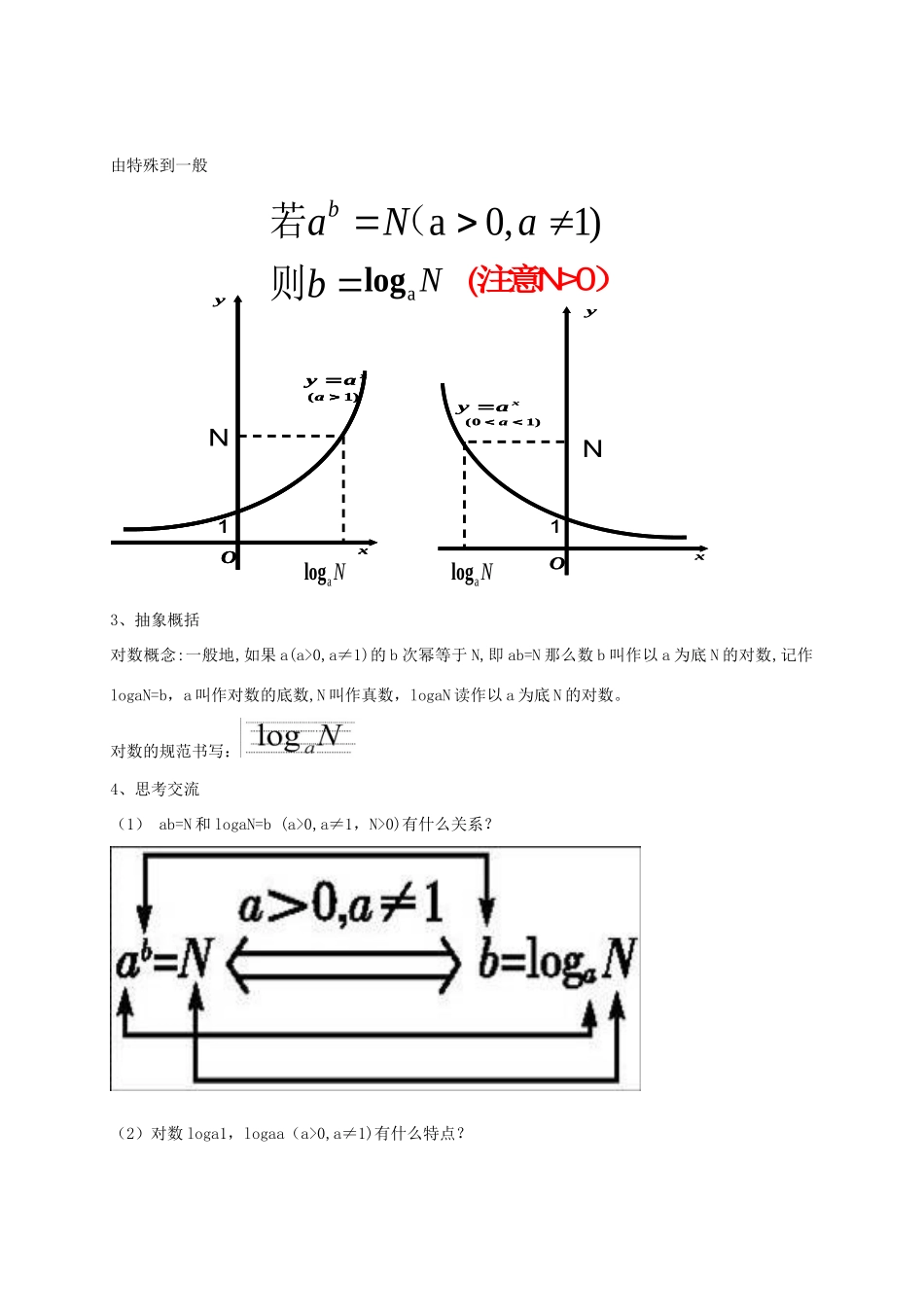
对数的概念一、三维目标1、知识与技能（1）理解对数的概念(2)能熟练的进行指数式与对数式的互化2、过程与方法学生经历有指数得到对数的过程，归纳对数的定义并体会定义的合理性。体会由特殊到一般、转化划归的思想3、情感、态度与价值观学生经历探索、研究、体会、感受对数概念的形成和发展过程，培养学生的探索精神和学习兴趣二、教学重难点重点：对数的定义难点：对数定义和对数符号的理解三、教学过程1、复习回顾指数函数的图像与性质2、新知探究1x2xyy1x2xyyx2xyy27log3x27x27log3xx2887由特殊到一般a0,1)baNab若（则aNlog(注意N>0）O1xay)1(axyO1xay)1(axO1xay)1(axyxyO1xay)10(axyO1xay)10(aaNlogaNlogNN3、抽象概括对数概念:一般地,如果a(a>0,a≠1)的b次幂等于N,即ab=N那么数b叫作以a为底N的对数,记作logaN=b，a叫作对数的底数,N叫作真数，logaN读作以a为底N的对数。对数的规范书写：4、思考交流（1）ab=N和logaN=b(a>0,a≠1，N>0)有什么关系？（2）对数loga1，logaa（a>0,a≠1)有什么特点？a3a0,1),NaNalog、（为什么aaa(0,1)......1......................a0,211)2bNNaNNbaaaloglog解：由式式把式代（入式得：（4）零和负数没有对数5、两个常用的对数(1)常用对数：我们通常将以10为底的对数叫作常用对数.为了简便,N的常用对数log10N简记作lgN例如：log105简记作lg5；log103.5简记作lg3.5(2)自然对数：在科学技术中常常使用以无理e=2.71828……为底的对数，以e为底的对数称为自然对数.为了简便，N的自然对数logeN简记作lnN例如：loge3简记作ln3；loge10简记作ln106例题讲解例1.使对数loga(-2a+1)有意义的a的取值范围为(B)A.a>1/2且a≠1B.00且a≠1D.a<1/2例2:将下列指数式写成对数式：（1）（2）（3）（4）456255log6254313273271log3438163416log8515aa15log5例3:将下列对数式写成指数式：（1）（2）（3）（4）12log1643log2435131log327lg0.111100.1-=311()327=53243=41()162-=例4.求下列各式的值（1）5log25（2）12log320=（4）10=（3）3log103（5）2.5log2.51=2=5=-ln1例5.计算：32log32（1）32log32（1）7log4log5552）（解析：（1）方法一：设32log32x,3232321x1x则方法二：32log32132log132(2)7log4log555554755loglog47287、课堂小结8、作业课本80页1、2、3题9、板书设计对数概念.......................例1.................................例4...............................................................................................................................................................................................................................................................................常用对数.......................例2................................例5.......................................................................................................................................................................................................................................................................................自然对数.......................例3............................................................................................................................................................................................10、课后反思