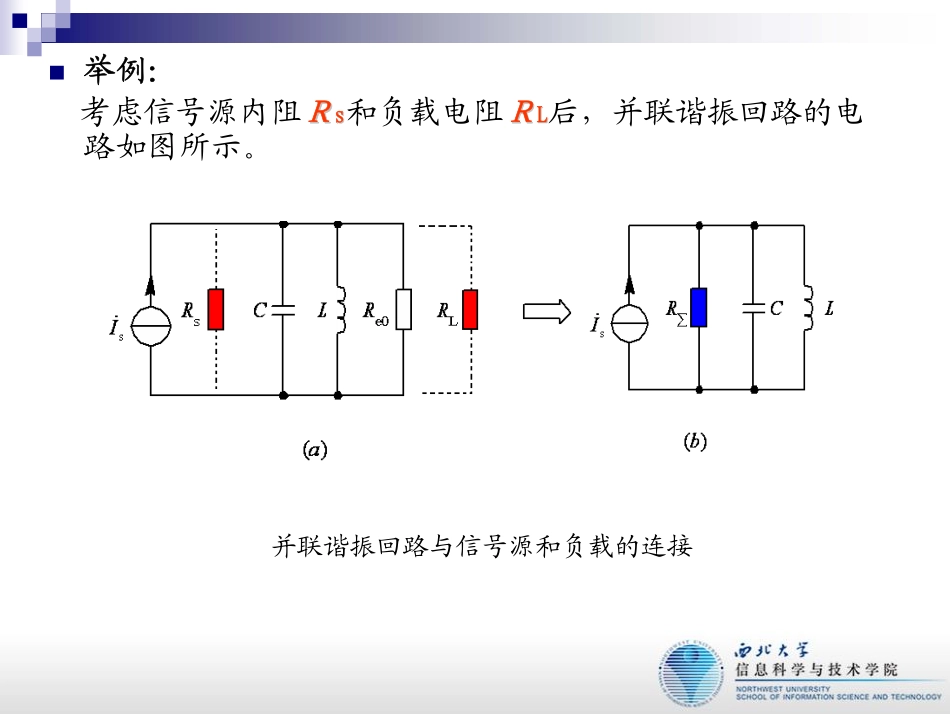
第三讲阻抗变换电路�阻抗变换电路是一种将实际负载阻抗变换为前级网络所要求的最佳负载阻抗的电路。�变换——“负载接入形式”上的变换。�作用:提高整个电路的性能。�举例:考虑信号源内阻RRss和负载电阻RRLL后,并联谐振回路的电路如图所示。并联谐振回路与信号源和负载的连接回路的空载Q值LRLgQee000001ωω==回路有载Q值LRLgQe001ωω∑∑==通频带eQfBW07.0=回路总电阻RΣ=Rs∥RL∥Re0考虑信号源内阻Rs和负载电阻RL后果:�Qe<Q0,且并联接入的Rs和RL越小,则Qe越小,回路选择性选择性越差。��谐振电压谐振电压随着谐振回路总电阻的减小而减小。�信号源内阻和负载不一定是纯电阻,还包括电抗电抗分量;因此总电抗受影响,回路的谐振频率谐振频率也受影响。�必须设法尽量消除接入信号源和负载对回路的影响。---〉通过“阻抗变换电路阻抗变换电路”接入负载就是一种有效解决方案�利用L、C元件的各自特性和LC回路的选频特性可以组成两大类阻抗变换电路(应用场合有所不同):1.纯电感或纯电容阻抗变换电路自耦变压器电路变压器阻抗变换电路电容分压式电路电感分压式电路2.LC选频匹配电路包括:L型、T型、π型1.纯电感或纯电容阻抗变换电路1)自耦变压器阻抗变换电路图(a)为自耦变压器阻抗变换电路,图(b)为考虑次级负载以后的初级等效电路;RL′是RL等效到初级的电阻。在图中,负载RL经自耦变压器耦合接到并联谐振回路上。假设自耦变压器损耗很小,可以忽略,则初、次级的功率P1、P2近似相等,且初、次级线圈上的电压U1和U2之比应等于匝数之比。设初级线圈与抽头部分次级线圈匝数之比N1∶N2=1∶n,(n=N2/N1,且n<=1)nUUPP1,2121==因为LLRUPRUP22221121,'21==所以LLLLRnRnUURR2'2221'11=⎟⎠⎞⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛=即结论:1、对于自耦变压器,n总是小于或等于1,所以,RL等效到初级回路后阻值增大,从而对回路的影响将减小。n越小,则RL′越大,对回路的影响越小。2、n的大小反映了外部接入负载(包括电阻负载与电抗负载)对回路影响大小的程度,可将n定义为接入系数。2)变压器阻抗变换电路sI�sI�2′LR′1′1′图(a)为变压器阻抗变换电路,图(b)为考虑次级负载以后的初级等效电路,RL′是RL等效到初级的电阻。若N1、N2分别为初、次级电感线圈匝数,则接入系数n=N2/N1。利用与自耦变压器电路相同的分析方法,将其作为无损耗的理想变压器看待,可求得RL折合到初级后的等效电阻为LLRnR2'1=3)电容分压式电路(b)sI�Rs(a)13RLLC1C22CsI�Rs13LC1C2LR′图a所示为电容分压式阻抗变换电路,图b所示是RL等效到初级回路后的初级等效电路。利用串、并联等效转换公式,先将RL和C2转换为串联形式,再与C1一起转换为并联形式,可以推导出RL折合到初级回路后的等效电阻为LLLRnRCCCR2221111=⎟⎟⎠⎞⎜⎜⎝⎛+=′211CCCn+=其中详细内容见《第二讲》具体推导过程分:先并到串;再串到并,如下图所示。()122"222212211LeLLLLeLLRQRCCRRRQRCRCωωωω=====步骤一:并联到串联的等效转换122""12'2""222"222"12122221212221212111111eLLLeLLLLLLCCCQCRRCCCRQRRRCCCRCCRCCCRCCCCCωωωωωω===+=⋅=⋅=⎛⎞⎜⎟+⎝⎠==⎛⎞⎛⎞⋅⋅⎜⎟⎜⎟++⎝⎠⎝⎠步骤二:串联到并联的等效转换又:所以:4)电感分压式电路sI�Rs(a)13RLCL22L1sI�Rs(b)13CLR′L图a为电感分压式阻抗变换电路,它与自耦变压器阻抗变换电路的区别在于L1与L2是各自屏蔽的,没有互感耦合作用。图b是RL等效到初级回路后的初级等效电路,L=L1+L2。LLLRnRLLLR2221211=⎟⎟⎠⎞⎜⎜⎝⎛+=′其中n是接入系数,在这里总是小于1。RL折合到初级回路后的等效电阻为例:某接收机输入回路的简化电路如所示。已知C1=5pF,C2=15pF,Rs=75Ω,RL=300Ω。为了使电路匹配电路匹配,线圈初、次级匝数比N1/N2应该是多少?负载RL等效到LC回路输入端的电阻RL′=Rs解:由图可见,这是自耦变压器电路与电容分压式电路的级联。RL等效到L两端的电阻为LLLLRRCCCRnR161212122"=⎟⎟⎠⎞⎜⎜⎝⎛+==RL″等效到输入端的电阻LLLLRNNRNNRnR22122121'16⎟⎟⎠⎞⎜⎜⎝⎛=′′⎟⎟⎠⎞...