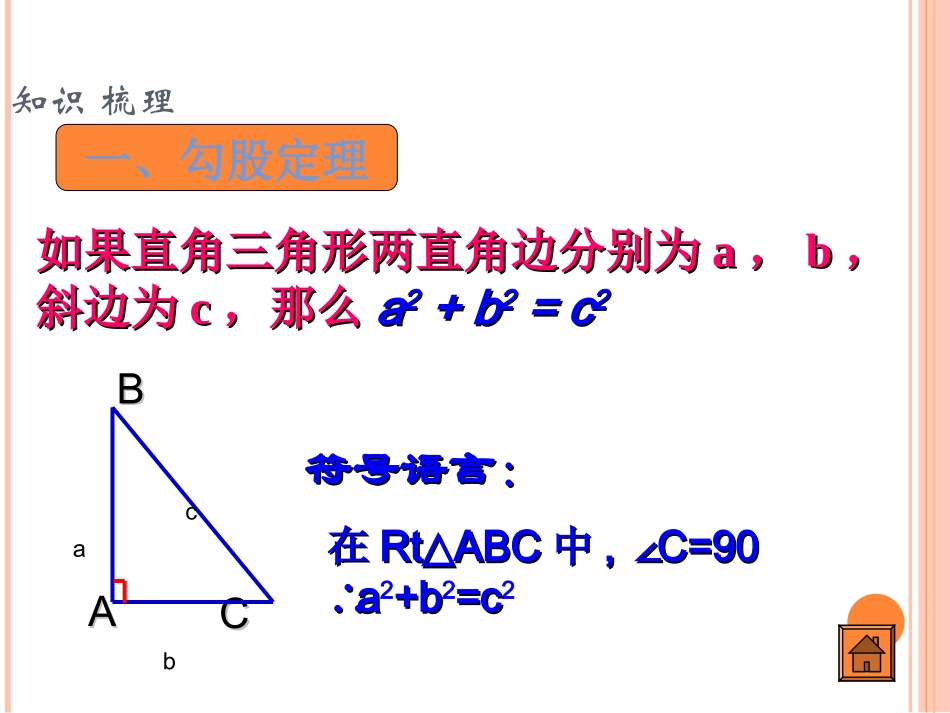
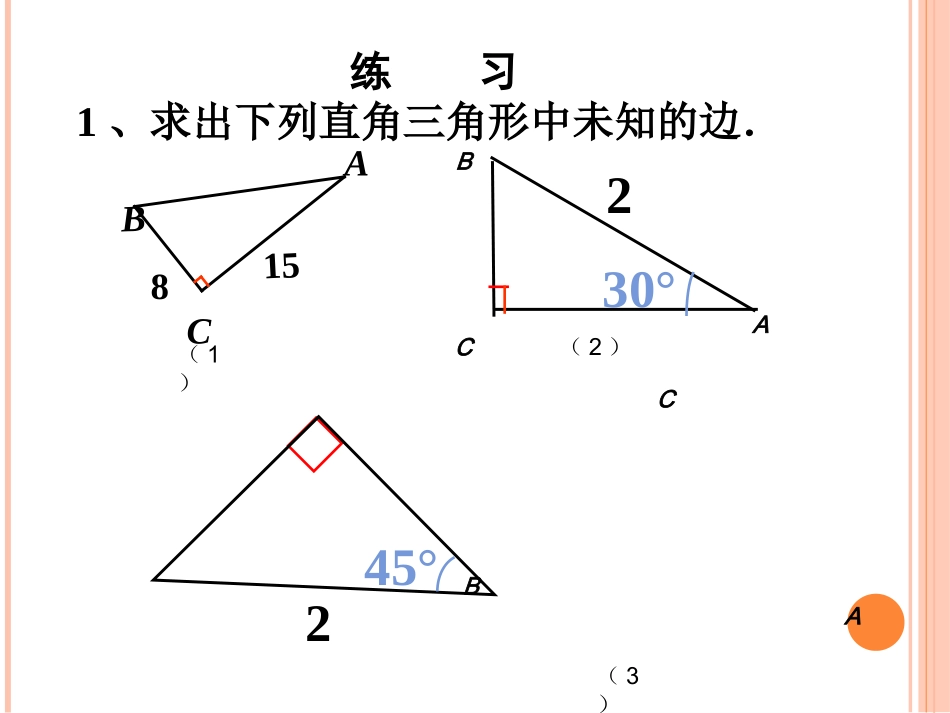
勾股定理复习知识梳理如果直角三角形两直角边分别为如果直角三角形两直角边分别为aa,,bb,,斜边为斜边为cc,那么,那么aa22+b+b22=c=c22一、勾股定理CCAABB符号语言:符号语言:在在RtABC△RtABC△中中,,∠∠C=90C=90∴∴aa2+b+b2=c=c2abc1、求出下列直角三角形中未知的边.8A15CB练习30°2245°(1)(2)(3)AABBCC2、你能在数轴上表示的点吗?17二、勾股定理的逆定理如果三角形的三边长如果三角形的三边长aa,,bb,,cc满足满足aa22+b+b22=c=c22,,那么这个三角形是直角三角形那么这个三角形是直角三角形互逆定理如果一个定理的逆命题经过证明是真命题如果一个定理的逆命题经过证明是真命题,,那么它也是一个定理那么它也是一个定理,,这两个定理叫做互逆定理这两个定理叫做互逆定理,,其中一个叫做另一个的逆定理其中一个叫做另一个的逆定理..CCAABB符号语言:符号语言:在△ABC中,∵∵aa2+b+b2=c=c2∴∴△ABC是直角三角形,∠∠C=90C=90abc(1)两条直线平行,内错角相等.(2)如果两个实数相等,那么它们的平方相等.(3)如果两个实数相等,那么它们的绝对值相等.(4)全等三角形的对应角相等.说出下列命题的逆命题.并判断逆命题成立?1.在已知下列三组长度的线段中,不能构成直角三角形的是()A5,12,13B2,3,C4,7,5D1,,5232.若△ABC中,AB=5,BC=12,AC=13,求AC边上的高.3、如图10所示,某港口P位于东西方向的海岸线上,“远航号”和“海天号”两艘轮船同时从港口离开,各自沿着一个固定的方向航行。“远航号”每小时航行16海里,“海天号”每小时航行12海里,它们离开港口一个半小时后,两船相距30海里,如果知道“远航号”的航行方向是东北方向,你能知道“海天号”是沿着哪个方向航行吗?“远航”“海天”,,,,,,523,ABCABCabcCBAABCABC2222中,的对边分别是下列判断错误的是()A.如果则ABC是直角三角形B.如果c=b-a,则ABC是直角三角形,且C=90C.如果(c+a)(c-a)=b,则ABC是直角三角形D.如果::::则是直角三角12、如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,B=90°∠,求四边形ABCD的面积┐DBAC341213变式有一块田地的形状和尺寸如图所示,试求它的面积。∟121334∟ABCD5专题一分类思想1.直角三角形中,已知两边长:直角边、斜边不确定时,应分类讨论。2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC∟D∟DABC1.已知:直角三角形的三边长分别是3,4,X,则此三角形的周长为_________。ABC1017817108专题二方程思想直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。1.小东拿着一根长竹竿进一个宽为3米的城门,他先横拿着进不去,又竖起来拿,结果竹竿比城门高1米,当他把竹竿斜着时,两端刚好顶着城门的对角,问竹竿长多少?x1m(x+1)3专题三折叠折叠和轴对称密不可分,利用折叠前后图形全等,找到对应边、对应角相等便可顺利解决折叠问题4、如图,小颖同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AB=10cm,BC=6cm,你能求出CE的长吗?BCADE变式:如图,小颖同学折叠一个直角三角形的纸片,使C与D重合,折痕为BE,若已知AB=10cm,BC=6cm,你能求出CE的长吗?CABDE例:折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求1.CF2.EC.ABCDEF810106X8-X48-X1.几何体的表面路径最短的问题,一般展开表面成平面。2.利用两点之间线段最短,及勾股定理求解。专题四展开思想例3,如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?2032AB20232323ABC∵AB2=AC2+BC2=625,∴AB=25.