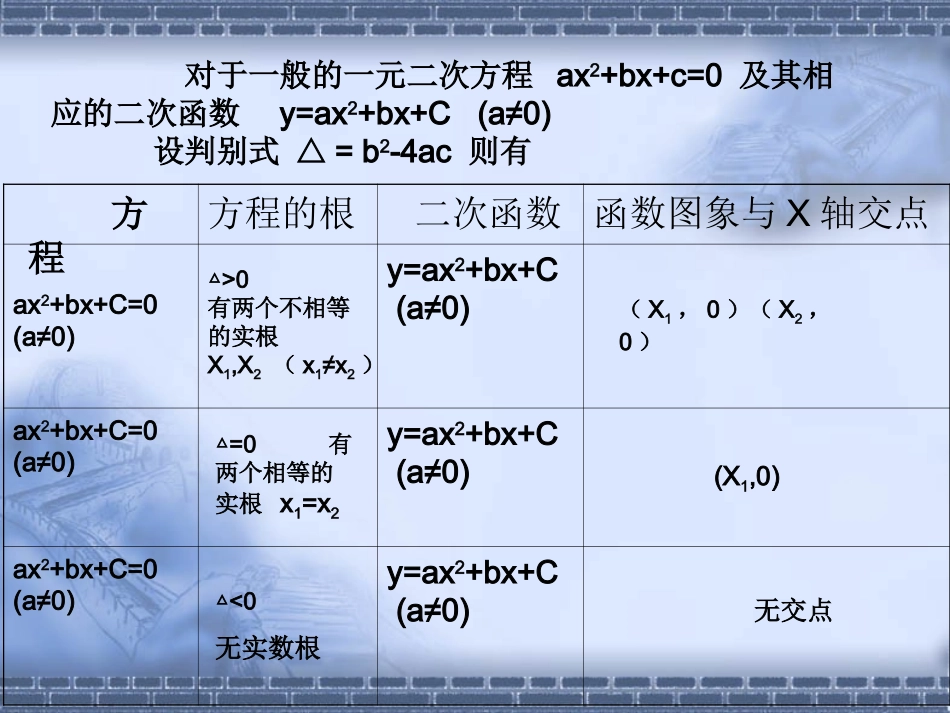
3.1.1方程的根与函数的零点用二次函数引出零点概念思考:一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?方程的根二次函数函数图象与X轴交点x2-2x-3=0y=x2-2x-3x2-2x+1=0y=x2-2x+1x2-2x+3=0y=x2-2x+3△>0X1=-1x2=3△=0x1=x2=1△<0无实数根(-1,0)(3,0)(1,0)无交点总结:如果一元二次方程有实数根,那么它的实数根就是相应二次函数图象与x轴交点的横坐标;如果一元二次方程没有实数根那么它相应的二次函数的图象与x轴没有交点.方程方程的根二次函数函数图象与X轴交点ax2+bx+C=0(a≠0)y=ax2+bx+C(a≠0)ax2+bx+C=0(a≠0)y=ax2+bx+C(a≠0)ax2+bx+C=0(a≠0)y=ax2+bx+C(a≠0)△>0有两个不相等的实根X1,X2(x1≠x2)△=0有两个相等的实根x1=x2△<0无实数根(X1,0)(X2,0)(X1,0)无交点方程对于一般的一元二次方程ax2+bx+c=0及其相应的二次函数y=ax2+bx+C(a≠0)设判别式△=b2-4ac则有上升引路问:能否把二次函数和一元二次方程的关系推广到一般的函数与相应方程的关系上呢?函数零点:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点意义:根据函数零点的定义,判断以下哪个是相应函数的零点例1.函数f(x)=x3-16x的零点是()A.(0,0),(4,0)B.0,4C.(-4,0),(0,0),(4,0)D.-4,0,4例2.求函数f(x)=x(x+2)(x-1)有无零点,有几个?有3个零点0,-2,1D函数f(x)=X2-2X-3计算f(1)与f(-2),f(2)与f(4)的值。f(1)·f(-2)<0f(2)·f(4)<0f(1)·f(-2)<0函数在区间(-2,1)内有零点x=-1,它是方程x2-2x-3=0的一个根.同样的f(2)·f(4)<0,函数在区间(2,4)内有零点x=3.它是方程的另一个根.所以我们可以总结出:如果函数f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a).f(b)<0那么y=f(x)在(a,b)内有零点.即.存在c(a,b),∈使f(c)=0,这个c也就是方程f(x)=0的根.我们发现:讨论:已知函数f(x)的图象是连续不断的,有如下x,f(x)的对应值表求函数在区间[1,6]上的零点数()A.至多2个B.至多3个C.恰有3个D.至少3个x123456F(x)123.5621.45-7.8211.57-53.76-126.49D由表3-1和图3.1—3可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内有零点。由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点。解:用计算器或计算机作出x、f(x)的对应值表(表3-1)和图象(图3.1—3)-4-1.30691.09863.38635.60947.79189.945912.079414.1972例题1求函数f(x)=lnx+2x-6的零点个数。123456789xxff((xx))..................x0-2-4-6105y241086121487643219本节课重点:1.函数零点的概念对于函数y=f(x),把使f(x)=0成立的叫做函数y=f(x)的零点2.函数的零点与方程根的关系实数x函数y=f(x)的零点就是方程f(x)=0的实数根,即函数y=f(x)的图象与x轴交点的.横坐标方程f(x)=0有实根函数y=f(x)图象x轴有交点函数y=f(x)有零点3.结论如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间内(a,b)内有零点。练习题:1.下列区间中函数f(x)=x3-2x+3有零点的是()A.(-3,-2)B.(-2,-1)C.(-1,0)D.(2,3)B连续函数f(x),在给定的区间(a,b)内,只要有f(a)·f(b)<0,那在区间(a,b)内就存在零点2.指出下列函数零点所在的大致区间:(1).f(x)=2x·ln(x-2)-3(2).f(x)=ex-1+4x-4解:(1)在函数定义域内,因为f(3)<0,f(4)>0,所以f(x)在区间(3,4)上有零点,又因为f(x)=2x·ln(x-2)-3在[2,+∞)上是增函数,所以f(x)在(3,4)上有且仅有一个零点。(2)因为f(0)<0,f(1)>0,所以f(x)在区间(0,1)上有零点,又因为f(x)=ex-1+4x-4在(-∞,+∞)上是增函数,所以f(x)在(0,1)上有且仅有一个零点。