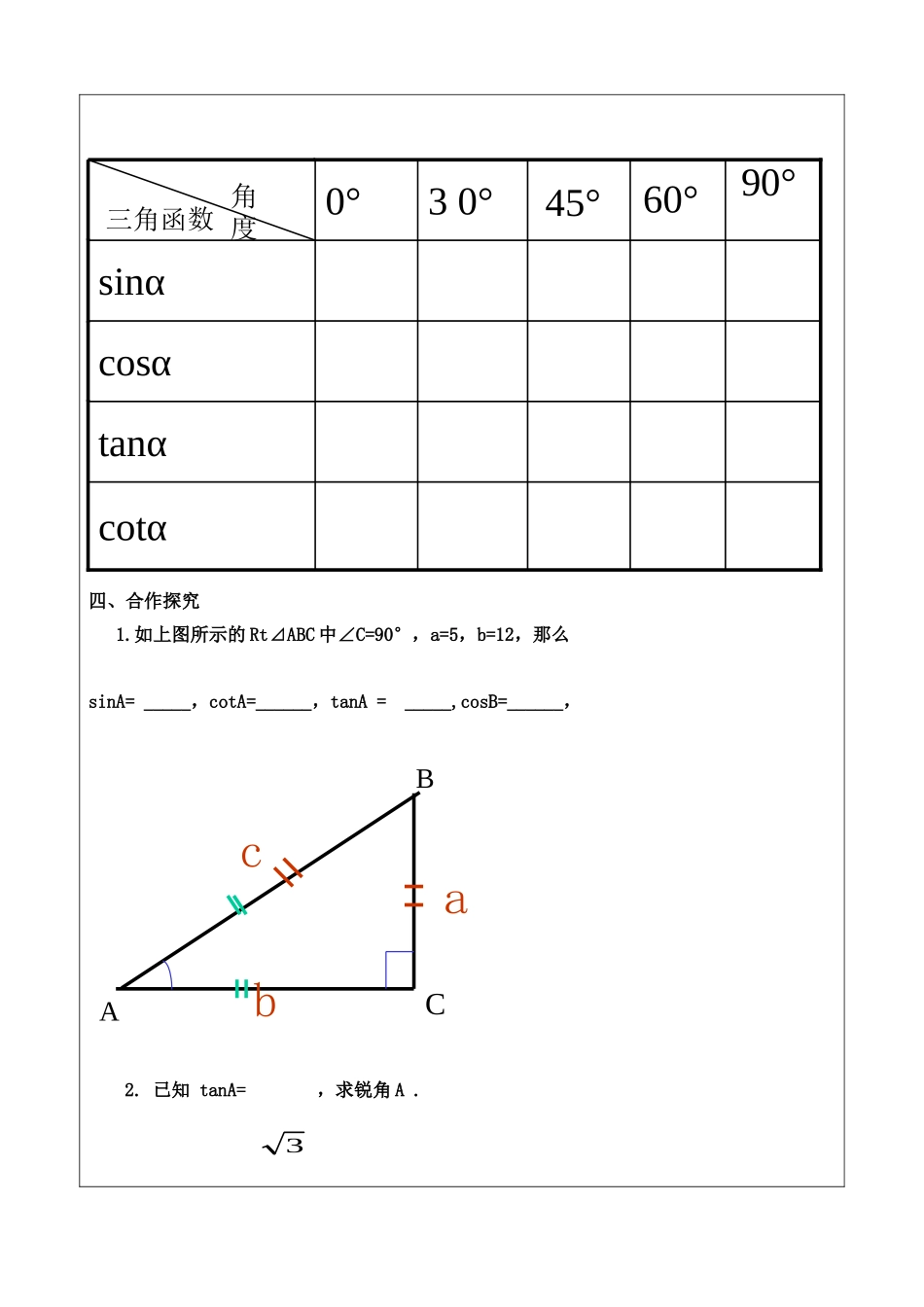
复习锐角三角函数导学单年级九科目数设计者郭改艳课题复习锐角三角函数学习目标、重点、难点1、熟记特殊角的三角函数值,并能根据这些值求对应特殊角的四个三角函数值。(重点)2、记住三角函数之间的关系。(难点)教学流程学习导航一、复习导入1.锐角三角函数的有关定义及关系如右图所示的Rt⊿ABC中∠C=90°,则1.正弦sinA=_______2.余弦cosA=_______3.正切tanA=_______4.余切cotA=_______复习导入思考探究知识回放合作探究实际应用二、思考探究1.(1)同角的正切与余切有何关系?(2)互为余角的正弦与余弦有何关系?条件:∠A为锐角tanA·cotA=_______sin2A+cos2A=_______sinA=_______cosA=_______tanA=_______cotA=_______三、知识回放1.特殊角的三角函数值ABCacb四、合作探究1.如上图所示的Rt⊿ABC中∠C=90°,a=5,b=12,那么sinA=_____,cotA=______,tanA=_____,cosB=______,2.已知tanA=,求锐角A.cotαtanαcosαsinα30°0°角度三角函数45°60°ABCacb390°3.已知2cosA-=0,求锐角A的度数.五、实际应用1.当锐角A>45°时,sinA的值()(A)小于(B)大于(C)小于(D)大于2.当锐角A>30°时,cosA的值()(A)小于(B)大于(C)小于(D)大于3.∠A为锐角,且tanA的值大于时,∠A()(A)小于30°(B)大于30°(C)小于60°(D)大于60°4.当∠A为锐角,且cotA的值小于时,∠A()(A)小于30°(B)大于30°(C)小于60°(D)大于60°5、当∠A为锐角,且cosA=那么()(A)0°<∠A≤30°(B)30°<∠A≤45°(C)45°<∠A≤60°(D)60°<∠A≤90°6、当∠A为锐角,且sinA=那么()(A)0°<∠A≤30°(B)30°<∠A≤45°(C)45°<∠A≤60°(D)60°<∠A≤90°33351313