八年级（下）分式方程2课件（改）VIP免费

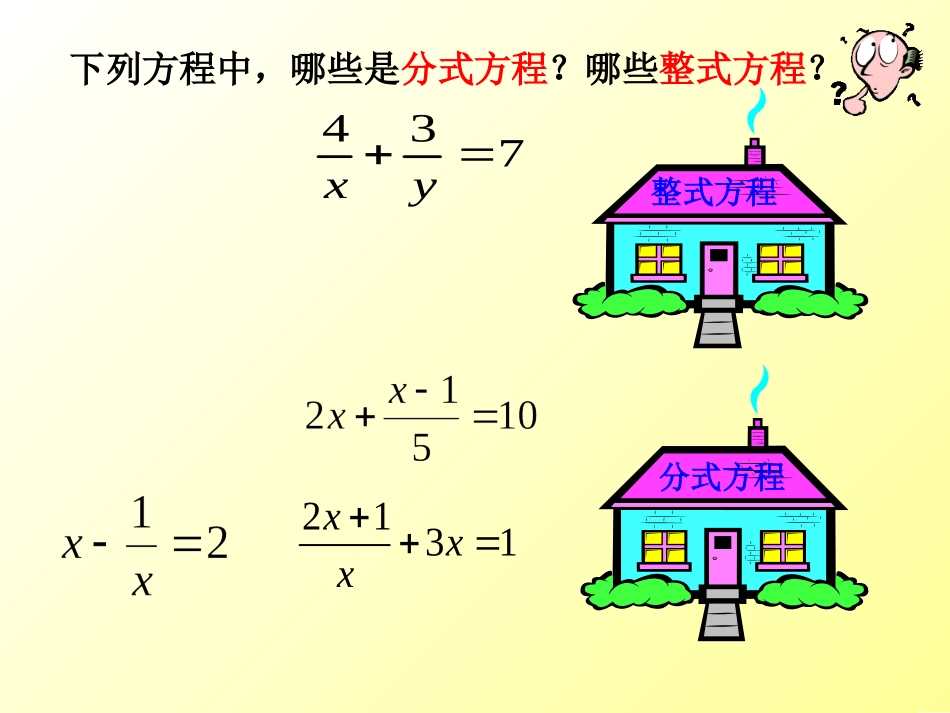
2131xxx437xy下列方程中，哪些是分式方程？哪些整式方程？整式方程分式方程（2）去括号,得解一元一次方程：解：（1）去分母,方程两边同乘以分母的最小公倍数6，得6113122)()(xx63324xx（3）移项,得121312xx32634xx（4）合并同类项,得77x（5）将未知数的系数化为1,得1x例1解方程：xx321解：方程两边同乘以最简公分母x(x-2)，得x=3(x-2)解这个方程，得x=3检验：将x=3代入原方程，得左边=1=右边所以，x=3是原方程的解.将分式方程转化为整式方程！注意：解分式方程要养成检验的好习惯.请认真解下列方程：4526004801xx)(131322xxx)(注意：解分式方程要养成检验的好习惯.解方程：22121xxx解：方程两边同乘以最简公分母x-2，得1-x=-1-2(x-2)解这个方程，得x=2检验：将x=2代入原分式方程，发现这时分母x-2和2-x的值为0，相应分式无意义。此时称x=2是原分式方程的增根。增根必舍去。所以，x=2不是原分式方程的解。所以，原分式方程无解。x=2是原方程的解吗？增根的定义增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.产生的原因:分式方程两边同乘以一个零因式零因式后,所得的根是整式方程的根,而不是分式方程的根.使分母的值为零的根·········判断的方法:将未知数的值代入原方程的最简公分母，若最简公分母等于零，则是增根；若最简公分母不等于零，则不是增根.例2解方程：解：方程两边同乘以最简公分母2x(x+3)，得x+3=4x解这个方程，得x=1检验：将x=1代入2x(x+3)所以，x=1是原方程的解.判断未知数的值是否为增根3221xx注意：解分式方程必须要检验未知数的值是否为增根.=8≠0解分式方程的一般步骤1、在方程的两边都乘以最简公分母，约去分母，化成整式方程.2、解这个整式方程.3、把整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解；否则，这个解不是原分式方程的解，必须舍去.4、写出原方程的根.解分式方程的思路是：分式方程整式方程转化一化二解三检验去分母（2）若关于x的方程有增根，则增根可能是.（1）如果关于x的方程有增根，则增根是.5352xmxxx=5使最简公分母的值为0的根313292xxxmx=3或x=-3（3）当m为何值时，方程会产生增根？5352xmxx增根是整式方程的根，不是分式方程的根.（4）当m为何值时，方程会产生增根？313292xxxm谢谢谢谢再再见见