同底数幂的乘法 (4)VIP免费

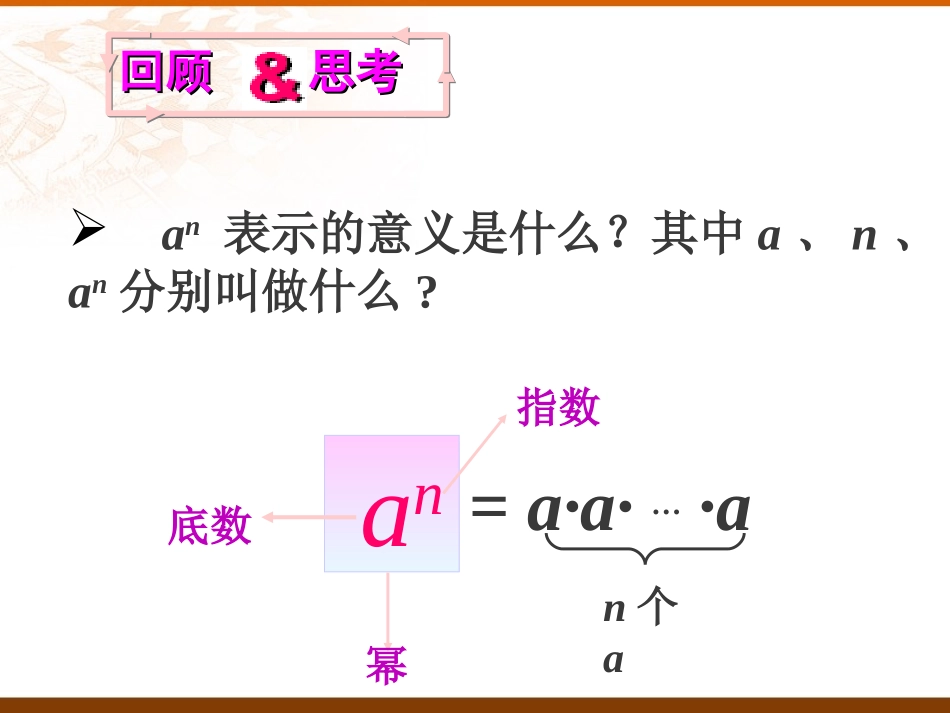
14.1.1同底数幂的乘法教学目标2.能运用同底数幂的乘法法则解决一些实际问题1.理解同底数幂的乘法法则．回顾思考回顾思考=a·a·…·an个aan表示的意义是什么？其中a、n、an分别叫做什么?an底数幂指数问题一种电子计算机每秒可进行次运算，它工作秒可进行多少次运算？1410310它工作秒可进行的运算次数是，3103141010观察这个算式，它的两个因式有何异同？同底数幂的乘法你知道了吗？我们观察可以发现，和这两个因数底数相同，是同底的幂的形式所以我们把这种运算叫做314101014103103141010（根据乘方的意义。）（根据乘方的意义。）(根据乘法结合律。)1017101010个1710你的依据是什么？你能算出3141010的结果吗？1031014314)101010()101010(1010个个合作探究合作探究(1)25×22=()×()=________________=2()；(2)a3×a2=()×()=_______________=a()；(3)5m·5n=()×()=5().2×2×2×2×22×22×2×2×2×2×2×27a×a×aa×aa×a×a×a×a5m+n请同学们根据乘方的意义理解，完成下列填空.思考：观察上面各题左右两边，底数、指数有什么关系？5×···×5m个5n个55×···×5am·an=m个an个a=a·a…a=am+n.(m+n)个a同底数幂相乘,底数不变,指数相加即am·an=am+n(m、n都是正整数)（a·a…a）（a·a…a）同底数幂的乘法法则:条件：①乘法②同底数幂结果：①底数不变②指数相加请同学们根据乘方的意义理解，完成下列填空.例1计算下列各式,结果用幂的形式表示.(2)a·a6；21+4+3a1+6xm+3m+1(1)x2·x5；(4)xm·x3m+1；x2+5=x7(3)2×24×23==28(2)a·a6==a7(3)2×24×23；(4)xm·x3m+1==y4m+1解(1)x2·x5=am·an·ap=am+n+p（m、n、p都是正整数)方法1am·an·ap=(am·an)·ap=am+n·ap=am+n+p方法2am·an·ap=(a·a·…·a)(a·a·…·a)(a·a·…·a)n个am个ap个a=am+n+p应用提高、拓展创新猜想（当m、n、p都是正整数时)am·an·ap=？练习：计算下列各式,结果用幂的形式表示.(1)b5×b；解:(1)b5×b=101+2+3-a2+6y2n+n+1(3)-a2·a6；(4)y2n·yn+1；b5+1=b6(2)10×102×103==106(3)-a2·a6==-a8(2)10×102×103；(4)y2n·yn+1==y3n+1例2:计算86)2()2)(1(52)71()71()2(52)())(3(baba11)4(mmyyy公式中的a可代表一个数、式子等.75252)71()71()71()71(⑵⑴14)86(86)2()2()2()2(解:7)52(52)()()()(babababa⑶)12()]1()1(1[11mmmmmyyyyy⑷练习下面的计算对不对？如果不对，怎样改正？（1）b5·b5=2b5（）（2）b5+b5=b10（）（3）x5·x5=x25()（4）y5·y5=2y10()（5）c·c3=c3()b5·b5=b10b5+b5=2b5x5·x5=x10y5·y5=y10c·c3=c4×××××你做对了吗填空：（1）8=2x，则x=；（2）8×4=2x，则x=；（3）3×27×9=3x，则x=.35623233253622×=3332××=计算解:（1）(a－b)2(a－b)=(a－b)2+1=(a－b)3.(1)(a－b)2(a－b).(3)210－22－23－24－25－26－27－28－29+2.(3)原式=210－29－28－27－26－25－24－23－22+2=2·29－29－28－27－26－25－24－23－22+2=29－28－27－26－25－24－23－22+2=…=22+2=6.应用提高、拓展创新(2)(x+y)3×(x+y).(2)(x+y)3×(x+y)=(x+y)3+1=(x+y)4.am·an=am+n(m，n都是正整数）.同底数幂的乘法性质：底数，指数.不变相加幂的意义:an=a·a·…·an个a注意：同底数幂相乘时你在知识上有哪些收获，你学到了哪些方法？am·an·ap=am+n+p（m、n、p都是正整数).