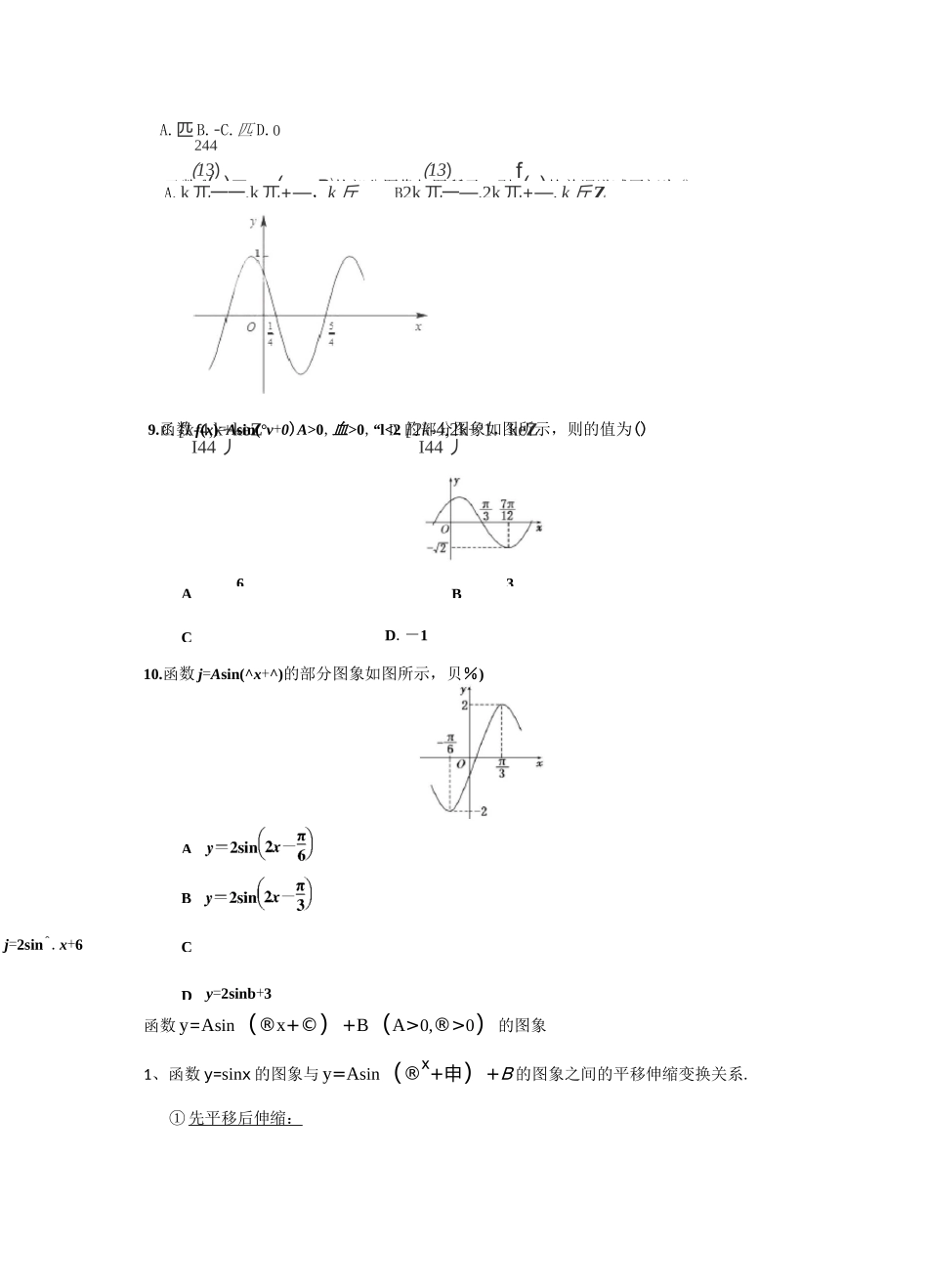
定义值最当x二2k兀+—2(keZ)时,y二1;max当x=2k—一—2(keZ)时,当x=2k—(keZ)时,y二1;当x=2k—+—max(keZ)时,y=-1.min既无最大值也无最小ym性奇偶奇函偶函奇函2k—-—,2k—+—22单调(keZ)上是增函数;2k—+—,2k—+3—22[2k—-—,2k—](keZ)是增函数;在bk—,2k—+—](keZ)上是减函数.—IT—7—^d在k————,k—+—I22丿对称对称中心(k—,0)(keZ)x=k—+2(keZ)对称中'k—+—,o](keZ)I2丿对称轴x=k—(keZ)无对称正弦函数、余弦函数和正切函数的图象与性质:周期(keZ)上是减函数;y二A7兀72K7—k兀+—,—k兀+—B兀5兀2k兀——,2k兀+——kGZ;CDk兀——,kK+——kGZ;12124.y=Icosxl的一个单调增区间是(Ann匕,2」B.[0,n]C3nn,D3nT,2nBCn1.最小正周期为n且图象关于直线x=3对称的函数是()A.y=2sin(2x+3C.y=2sin(J2+32.函数y=仆谆一2x)的单调减区间为兀3•函数y二smq-2x)的单调递减区间是()5.如果函数y=3cos(2x+0)的图象关于点伴,0)对称,那么⑷I的最小值为(A.D.6.已知函数f(x)二sm(2x--)(xGR)下列结论错误的是()2A.函数f(x)的最小正周期为兀B.函数f(x)是偶函数兀兀C.函数f(x)的图象关于直线x二对称D.函数f(x)在区间[0,〒]上是增函数427.已知y=cos(®x+^)(co>0,屮G〔0,2兀))的部分图象如图所示,则9=()BD(13)A.k兀一一,k兀+—,k丘(13)B2k兀一—,2k兀+—,k丘ZC.[k-4,k+keZI44丿D.[2k-4,2k+31,keZI44丿CCDy=2sinb+3A.匹B.-C.匹D.0244D.-110.函数j=Asin(^x+^)的部分图象如图所示,贝%)函数y=Asin(®x+©)+B(A>0,®>0)的图象1、函数y=sinx的图象与y=Asin(®x+申)+B的图象之间的平移伸缩变换关系.①先平移后伸缩:8.函数f(x)二cos(ex+P)的部分图像如图所示,则f(x)的单调递减区间为().9.函数f(x)=Asin(°v+0)A>0,血>0,“l<2的部分图象如图所示,则的值为()A6B3ABj=2sin^.x+6y=sinx平移|屮|个单位y=sin(x+9)►(左加右减)横坐标不变亍y=Asin(x+9)纵坐标变为原来的A倍纵坐标不变.y=Asinx+“横坐标变为原来的1丄1倍平移IBI个单位.y=Asin(①x+9)+B上加下减)②先伸缩后平移:y=sinx横坐标不变*y=Asinx纵坐标变为原来的A倍纵坐标不变.y=Asin®x横坐标变为原来的1丄1倍平移里个单位y=AsinGx+9)-^-1(左加右减)平移IBI个单位.y=Asin(3x+9)+B上加下减)1.将函数/(对二或“卜+劭的图象上各点的纵坐标不变,横坐标伸长到原来的2倍,所得图象的一条对称轴方程可能是()AnA-x=_12nB.兀―12c.兀=3c2nD.x—3A.y=sin(2x-s)(xR)B.y=sin(扌+:)(XWR)C.y=sin(2x+H)(x£R)D.y=sin(2x+互)(xWR)3AC向右平移丁个单位6向左平移丁个单B、向右平移右个单位12冗D、向左平移百个单位x4.要得到函数y=cos(_2冗A.向左平移〒个单位2冗J6.要得到函数y二cos2x的图2.把函数y=sinx(xWR)的图像上所有的点向左平移亍个单位长度,再把所得图像上所有点的横坐标缩短到原来的2(纵坐标不变),得到的图像所表示的函数是()2要得到函数y二2血力的图像,只需将y3Sin2X—COS2X的图像()x兀x(2一—)的图象,只需将y=sin2的图象242冗B.同右平移〒个单位2冗D.向右平移〒个单位45.将函数y=3sin(2x+§的图像向右平移于个单位长度,所得图像对应的函数(nnc.在区间石,"3_|上单调递减nnD.在区间石,亍]上单调递增只需将函数y二sin(2x+春[的图像沿x轴(k3丿A•向左平移个单位12冗C.向右平移个单位6B.向左平移个单位6冗D.向右平移个单位上单调递减n7n上单调递增7•将函数fC)=sin(2x+9)的图象向左平移扌个单位,所得到的函数图象关于y轴对称,8则9的一个可能取值为()3兀兀c兀A.B.C.0D.-4448•将函数y二sin(2x+;)的图象向右平移个单位,再纵坐标不变,横坐标变为原来的266倍,所得新图象的函数解析式是()A.y=sin4xB.y=sinxC.y=sin(4x-—)D.y=sin(x-—)66