电场强度与电势梯度的关系14VIP免费

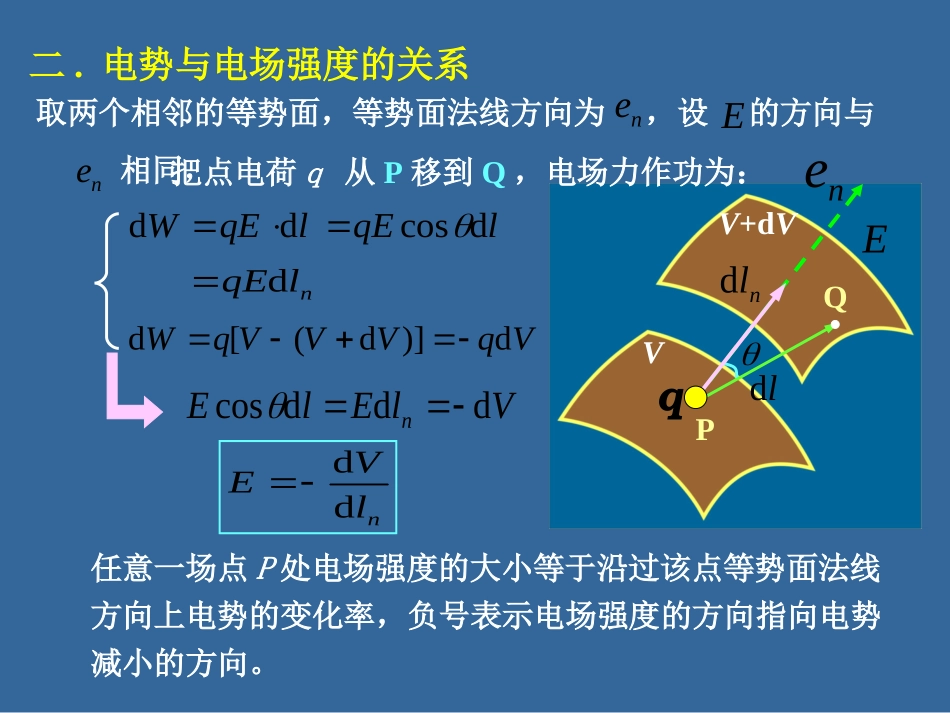
场强与电势梯度的关系一、等势面等势面：电场中电势相等的点所构成的面。下面我们来看几种典型的等势面。在电场中，一般来说，电势应该是空间位置坐标的函数，是逐点变化的，但是总会有一些点的电势是相等的。等势面的性质⑴等势面与电场线处处正交，电场线指向电势降落的方向，即沿着场强的方向电势降落。因此，在等势面上移动电荷时，电场力不作功，电荷的电势能不变。（2）规定：电场中任意两相邻等势面间的电势差必须相等，由于场强大的地方产生相同的电势差所需的距离小，而场强小的地方产生相同的电势差所需的距离大，这样就会形成场强大的地方等势面密集，而场强小的地方等势面稀疏。VV+dV二.电势与电场强度的关系取两个相邻的等势面，等势面法线方向为nlqEdlqElEqWdcosddVqVVVqWd)]d([dnlVEddVlElEndddcosEnld任意一场点P处电场强度的大小等于沿过该点等势面法线方向上电势的变化率，负号表示电场强度的方向指向电势减小的方向。ne把点电荷q从P移到Q，电场力作功为：ne，设E的方向与ne相同，PQldqVV+dVnldPQldqnlVEddEnennelVEddVV+dVnldPQldqgradV定义：电场中任一点的电势梯度矢量的大小等于电势函数沿着等势面法线方向的导数，方向总是沿着等势面的法线且指向电势升高的方向。nnelVgradVdd某点的电场强度等于该点电势梯度的负值，这就是电势与电场强度的微分关系。gradVelVEnnddVlElθEndddcos另一种理解VlElddlVElddnllddnlVlVdddd电场强度在l方向的投影等于电势沿该方向变化率的负值电势沿等势面法线方向的变化率最大neVV+dVnldPQldqE在直角坐标系中xVExyVEyzVEz)(kzVjyVixVEkzVjyVixVgradV电势梯度nnelVgradVdd例求（2，3，0）点的电场强度。已知22766zyxxu解66)126(xyxuEx2462xyuEyjijEiEEyx2466014zzuEz例、利用电场强度与电势的关系求电偶极子电场中任一点P的电场强度210122010214)(44rrrrqrqrquuuPlrcos12lrr221rrr20cos4rlquPlqp由于3041rrpuP),(yxPr1r2rlOqqXYx),(yxPr1r2rlOqqXYx20π41rpεVπθ0V2πθ20π41rpεV0θ),(yxPr1r2rlOqqXYxxVEx2/522220)(2π4yxxyεpyVEy2/5220)(3π4yxxyεp22yxEEE2222/1220)()4(π4yxyxεp2222/1220)()4(π4yxyxεpE0y301π42xεpE0x301π4yεpE),(yxPr1r2rlOqqXYxRdq例1．利用场强与电势梯度的关系，计算均匀带电细圆环轴线上一点的场强。yzxxpr例、利用电场强度与电势的关系求通过半径为R的均匀带电圆平板中心且垂直平面的轴线上任意点的电场强度.设电荷面密度为。rrqdπ2d)(2220xRxεRrxrrεV0220dπ2π41Pxox2/122)(rxrdrRPxox2/122)(rxrdrRxVE)1(2220Rxxε)(2220xRxεV课堂练习利用场强与电势梯度的关系求均匀带电细杆中垂线上P点的电场强度。已知细杆的的电量为q,长度为L。yPLXOxdxyLPyxyxdxr)4/2/ln(242202/2/220yLyLLqxydxLqVLLP求电场强度的三种方法求电场强度的三种方法从点电荷场强公式出发，根据场强叠加原理利用高斯定理利用电势梯度与电场强度的关系根据已知的场强分布，按定义计算"0"PPldEV电势计算的两种方法：由点电荷电势公式，利用电势叠加原理计算rqV04