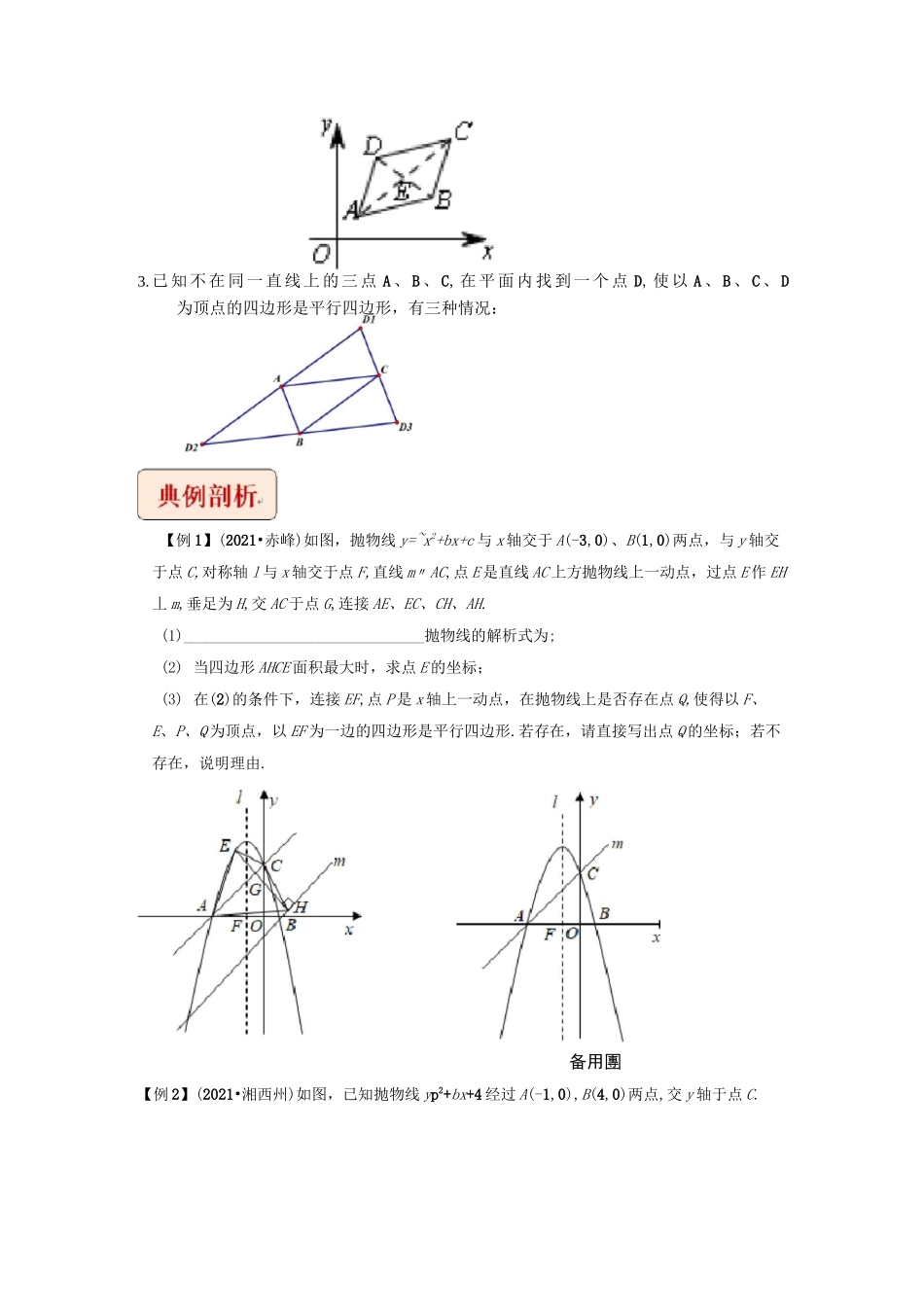
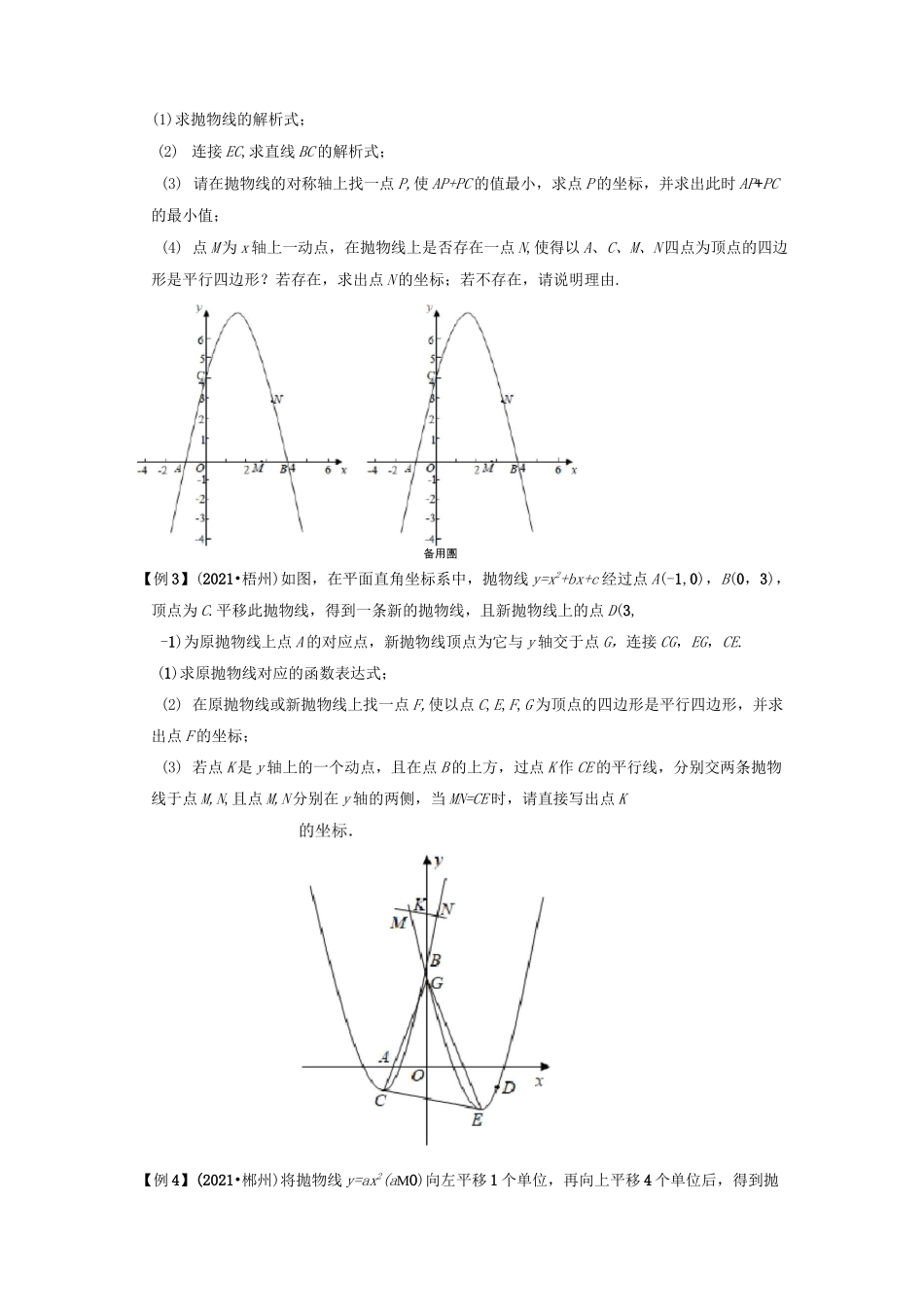
专题6二次函数与平行四边形存在性挑战2022年中考数学压轴题之学霸秘笈大揭秘专题6二次函数与平行四边形存在性问题考法综述亠:)以二次函数为载体的平行四边形存在性问题是中考的热点难点之一,其图形复杂,知识覆盖面广,综合性较强,对学生分析问题和解决问题的能力要求高.对这类题,常规解法是先画出平行四边形,再依据“平行四边形的一组对边平行且相等”或“平行四边形的对角线互相平分”来解决.由于先要画出草图,若考虑不周,很容易漏解.方法揭秘解决抛物线中的平行四边形存在性问题,常用的结论和方法有:线段中点坐标公式、平行四边形顶点坐标公式、画平行四边形.1.平面直角坐标系中,点A的坐标是(x,y),点B的坐标是(X,y),则线段AB的1122x+xy+y中点坐标是(亠22,巧2).2.平行四边形ABCD的顶点坐标分别为(x,y)、(x,y)、(x,y)、(x,y),则AABBCCDDx+x=x+x,ACBDy+y二y+y.ACBD【刚:L】(2021-赤峰中考真[»](2021^州中考卓题)【例5】(2021*海南中考真【例2】(2G21*湘西州中考克【例引(2021^®+)中考亘题}3.已知不在同一直线上的三点A、B、C,在平面内找到一个点D,使以A、B、C、D为顶点的四边形是平行四边形,有三种情况:【例1】(2021•赤峰)如图,抛物线y=~x2+bx+c与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C,对称轴l与x轴交于点F,直线m〃AC,点E是直线AC上方抛物线上一动点,过点E作EH丄m,垂足为H,交AC于点G,连接AE、EC、CH、AH.(1)________________________________抛物线的解析式为;(2)当四边形AHCE面积最大时,求点E的坐标;(3)在(2)的条件下,连接EF,点P是x轴上一动点,在抛物线上是否存在点Q,使得以F、E、P、Q为顶点,以EF为一边的四边形是平行四边形.若存在,请直接写出点Q的坐标;若不存在,说明理由.备用團【例2】(2021•湘西州)如图,已知抛物线yp2+bx+4经过A(-1,0),B(4,0)两点,交y轴于点C.(1)求抛物线的解析式;(2)连接EC,求直线BC的解析式;(3)请在抛物线的对称轴上找一点P,使AP+PC的值最小,求点P的坐标,并求出此时AP+PC的最小值;(4)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.备用團【例3】(2021•梧州)如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(-1,0),B(0,3),顶点为C.平移此抛物线,得到一条新的抛物线,且新抛物线上的点D(3,-1)为原抛物线上点A的对应点,新抛物线顶点为它与y轴交于点G,连接CG,EG,CE.(1)求原抛物线对应的函数表达式;(2)在原抛物线或新抛物线上找一点F,使以点C,E,F,G为顶点的四边形是平行四边形,并求出点F的坐标;(3)若点K是y轴上的一个动点,且在点B的上方,过点K作CE的平行线,分别交两条抛物线于点M,N,且点M,N分别在y轴的两侧,当MN=CE时,请直接写出点K【例4】(2021•郴州)将抛物线y=ax2(aMO)向左平移1个单位,再向上平移4个单位后,得到抛CCQBO副Q【例5】(2021•海南)已知抛物线y=ax2+x+c与x轴交于A、B两点,与y轴交于C点,且点A的坐标为(-1,0)、点C的坐标为(0,3).1)求该抛物线的函数表达式;备用物线H:y=a(x-h)2+k.抛物线H与x轴交于点A,B,与y轴交于点C.已知A(-3,0),点P是抛物线H上的一个动点.(1)求抛物线H的表达式;(2)如图1,点P在线段AC上方的抛物线H上运动(不与A,C重合),过点P作PD丄AB,垂足为D,PD交AC于点Z作PF丄AC,垂足为F,求APEF的面积的最大值;(3)如图2,点Q是抛物线H的对称轴l上的一个动点,在抛物线H上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.(2)如图1,若该抛物线的顶点为P,求APBC的面积;(3)如图2,有两动点D、E在ACOB的边上运动,速度均为每秒1个单位长度,它们分别从点C和点B同时出发,点D沿折线COB按CH方向向终点B运动,点E沿线段BC按B-C方向向终点C运动,当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒,请解答下列问题:①当t为何值时,ABDE的面积等于p亍;②在点D、E运动过程中,该抛物线上存在点F,使得依次连接AD、DF、FE、EA得到的四边形ADFE是平行四边形,请直接写出所有符合条件的点F的坐标.满分训练,\/1.(...