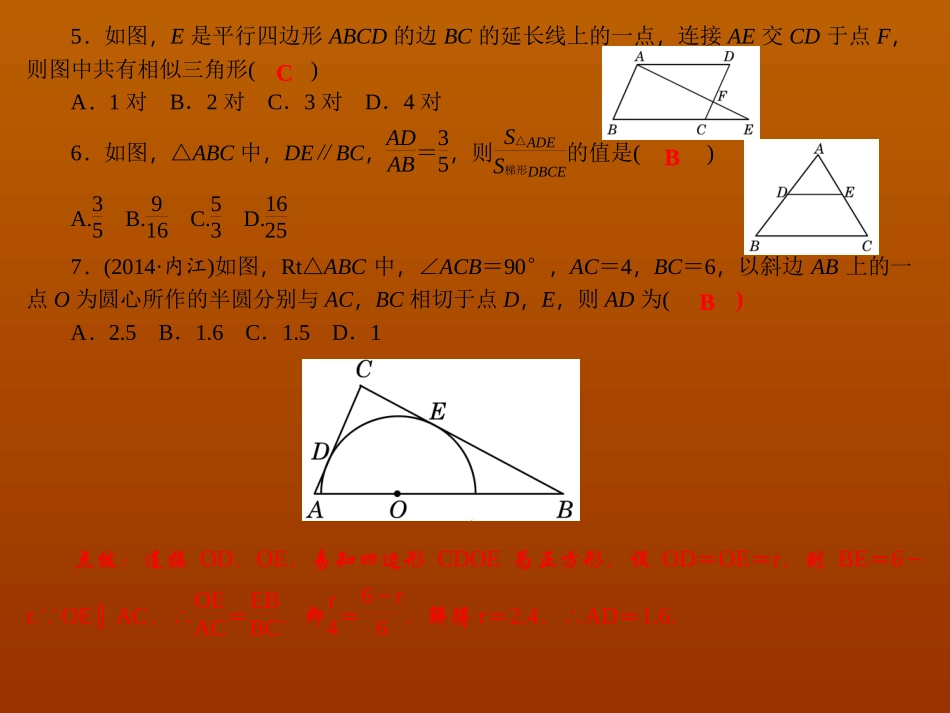
检测内容:第二十七章一、选择题(每小题3分,共30分)1.下面不是相似图形的是()2.如下左图,P是△ABC的AC边上一点,连接BP,以下条件中不能判定△ABP∽△ACB的是()A.AB2=AP·ACB.AC·BC=AB·BPC.∠ABP=∠CD.∠APB=∠ABC3.如下中图,身高为1.6米的某学生想测量学校旗杆的高度,当她在C处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2米,BC=8米,则旗杆的高度是()A.6.4米B.7米C.8米D.9米4.如上右图,E(-4,2),F(-1,-1),以O为位似中心,按比例尺1∶2,把△EFO缩小,则点E的对应点E′的坐标为()A.(2,-1)或(-2,1)B.(8,-4)或(-8,4)C.(2,-1)D.(8,-4)ABCA5.如图,E是平行四边形ABCD的边BC的延长线上的一点,连接AE交CD于点F,则图中共有相似三角形()A.1对B.2对C.3对D.4对6.如图,△ABC中,DE∥BC,ADAB=35,则S△ADES梯形DBCE的值是()A.35B.916C.53D.16257.(2014·内江)如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC,BC相切于点D,E,则AD为()A.2.5B.1.6C.1.5D.1点拨:连接OD,OE,易知四边形CDOE为正方形,设OD=OE=r,则BE=6-r.OEAC ∥,∴OEAC=EBBC,即r4=6-r6,解得r=2.4,∴AD=1.6.CBB8.(2014·丽水)如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=12DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为()A.-12xx-4B.-2xx-1C.-3xx-1D.-8xx-4点拨:过F点作FHBC⊥于H,易证DBEEHF△≌△,则BE=FH=x,EH=2x,又FHAD ∥,∴FHAB=CHBC,即x4=y-3xy,∴y=-12xx-4.9.如图,在已建立直角坐标系的4×4的正方形方格中,△ABC是格点三角形(三角形的三个顶点是小正方形的顶点),若以格点P,A,B为顶点三角形与△ABC相似(全等除外),则格点P的坐标是()A.(1,4)B.(3,4)C.(3,1)D.(1,4)或(3,4)AD10.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=14CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF,其中正确的个数为()A.1个B.2个C.3个D.4个点拨:设CF=a,则DF=3a,BE=EC=2a,AB=AD=DC=4a,∴ABBE=FCBC=12,∴△ABE∽△ECF,易知AEF∠=90°,勾股定理知AE=25a,EF=5a,∴ABBE=AEEF=12,∴△ABE∽△AEF,而ADDF≠ECFC,∴△ADF∽△ECF不成立,AE≠2BE,∴∠BAE≠30°.二、填空题(每小题3分,共24分)11.如果x2=y3=z4≠0,那么x+2y+3z3x+2y-2z的值是__.12.在△ABC中,AB=8,AC=6,在△DEF中,DE=4,DF=3,要使△ABC与△DEF相似,则需要添加一个条件是__.(写出一种情况即可)B5∠A=∠D(或BCEF∶=21)∶13.如图,AB∥CD,AD与BC相交于点O,OA=4,OD=6,则△AOB与△DOC的周长比是__.14.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=__m.15.如图,点D,E分别在△ABC的边AB,AC上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE的长为__.16.如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于点M,N,给出下列结论:①△ABM≌△CDN;②AM=13AC;③DN=2NF;④S△AMB=12S△ABC.其中正确的结论是__.(填序号)23∶5.54①②③17.(2013·贵阳)如图,点M是Rt△ABC的斜边BC上异于B,C的一点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有__条.18.如图,矩形AOCB的两边OC,OA分别位于x轴、y轴上,点B的坐标为B(-203,5),D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是__.点拨:过点E作EFCO⊥于点F,由折叠知EO=AO=5,BC=5,CO=203,由勾股定理知BO=253, EF∥BC,∴EF5=5253=FO203,解得EF=3,FO=4,∴E(-4,3),∴反比例函数解析式为y=-12x.3y=-12x三、解答题(共66分)19.(8分)如...