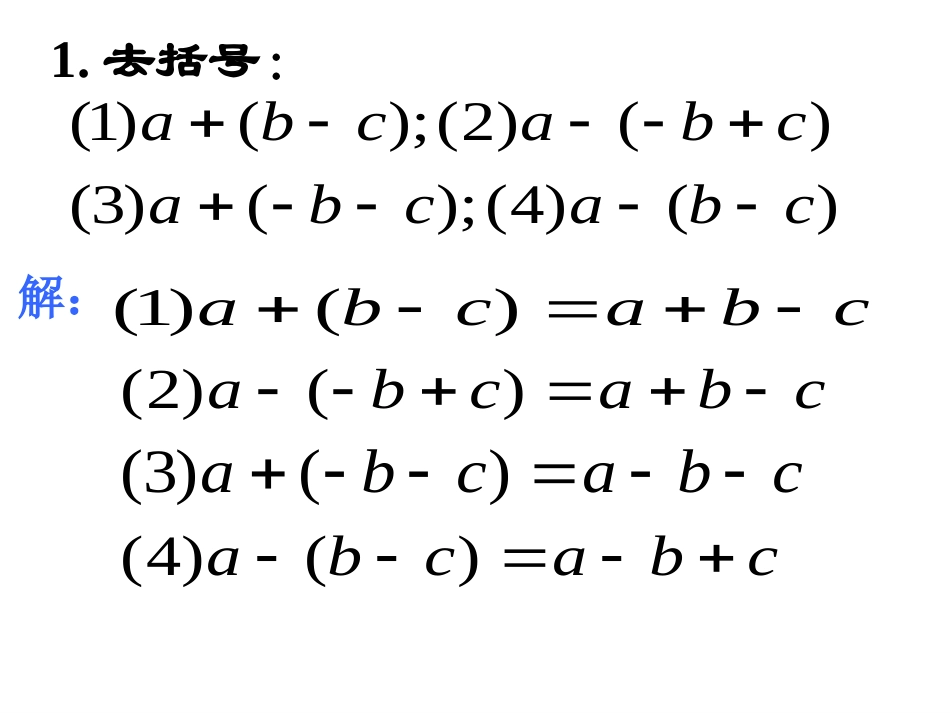添括号法则课件VIP免费

添括号法则添括号法则)()4();()3()()2();()1(cbacbacbacba1.去括号：cbacba)()1(cbacba)()2(cbacba)()3(cbacba)()4(解：2.去括号的法则是什么？•括号前面是“+”号，把括号和它前面的“+”号去掉，括号里各项都不改变正负号。•括号前面是“-”号，把括号和它前面的“-”号去掉，括号里各项都改变正负号。上面是根据去括号法则，由左边式子得右边式子，现在我们把上面四个式子反过来(1)a+b-c=a+(b-c)(2)a-b-c=a+(-b-c)(3)a+b-c=a-(-b+c)(4)a-b+c=a-(b-c)3a+b–c=a+(b–c)符号均没有变化a+b–c=a–(–b+c)符号均发生了变化添上“+()”,括号里的各项都不变符号；添上“–()”,括号里的各项都改变符号．观察1、下列各式，等号右边添的括号正确吗？若不正确，可怎样改正？2222236(236)236(236)23(23)()xxxxxxxxabcabcmnabmnab（１）（２）（３）（４）检验方法：用去括号法则来检验添括号是否正确2、做一做：.在括号内填入适当的项：(1)x²–x+1=x²–()；(2)2x²–3x–1=2x²+()；(3)(a–b)–(c–d)=a–().x–1–3x–1b+c–d3.填空:2xy²–x³–y³+3x²y=+()=–()=2xy²–()+3x²y=2xy²+()+3x²y=2xy²–()–x³2xy²–x³–y³+3x²y–2xy²+x³+y³–3x²yx³+y³–x³–y³y³–3x²y运用乘法公式计算:(1)(x+2y-3)(x-2y+3);(2)(a+b+c)2.解:(1)(x+2y-3)(x-2y+3)=[x+(2y–3)][x-(2y-3)]=x2-(2y-3)2=x2-(4y2-12y+9)=x2-4y2+12y-9.(2)(a+b+c)2=[(a+b)+c]2=(a+b)2+2(a+b)c+c2=a2+2ab+b2+2ac+2bc+c2=a2+b2+c2+2ab+2bc+2ac.用简便方法计算：(1)214a＋47a＋53a；(2)214a–39a–61a．7解:(1)214a＋47a＋53a=214a＋(47a＋53a)=214a＋100a=314a(2)214a–39a–61a=214a–(39a＋61a)=214a–100a=114a15,1822yxyxyx当时，求的值。222yxyx3、在横线上添上适当的代数式，使等式成立22222222(1)()_____(2)()_____(3)()()_______abababababab4.公式变形的应用：2222221,2,________29,8,________)25,()16,________abababxyxyxyxyxyxy（1）已知则。（）已知则。（3）已知(则。2222416_______2425___________12,_____.(4)41xaxaxkxyykxxmmx（1）已知，是完全平方式，则。（）已知，是完全平方式，则。(3)是完全平方式则请把添加一项后是完全平方式，可以添加____________.5.完全平方式1、利用公式进行计算：22(1)(2)(2)(2)(2)(2)(3)(23)(4)(2)xyxyabbaabxy2、化简求值：22213)(1)(2),1(2)()()()213,3xxxxabababbab（）(其中其中7.计算：2(1)()(2)()()(3)()()abcabcabcabcabc思考题：243212222)()()()().(1xxxxedcbadcbacbaba(1)3x²y²–2x³+y³(2)–a³+2a²–a+1(3)3x²–2xy²+2y²4.给下列多项式添括号，使它们的最高次项系数为正数.如:–x²+x=–(x²–x);x²–x=+(x²–x)练一练=+()=–()=–()=–()93x²y²–2x³+y³a³–2a²+a–1–3x²+2xy²–2y²2xy²–3x²–2y²1.用简便方法计算：(1)117x+138x–38x;(2)125x–64x–36x;(3)136x–87x+57x.