直线与双曲线的位置关系VIP免费

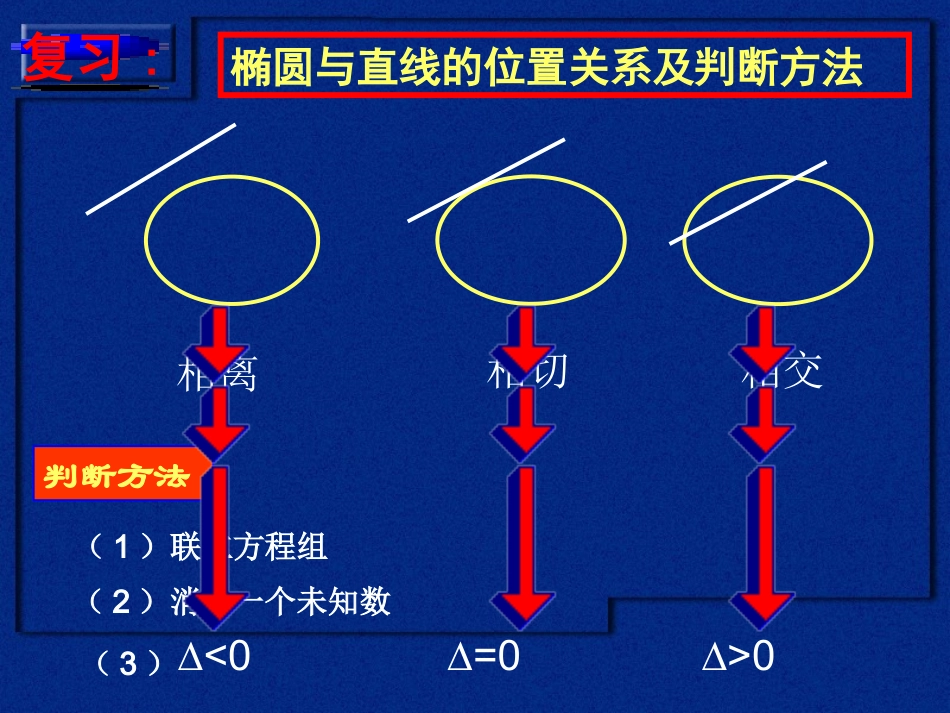
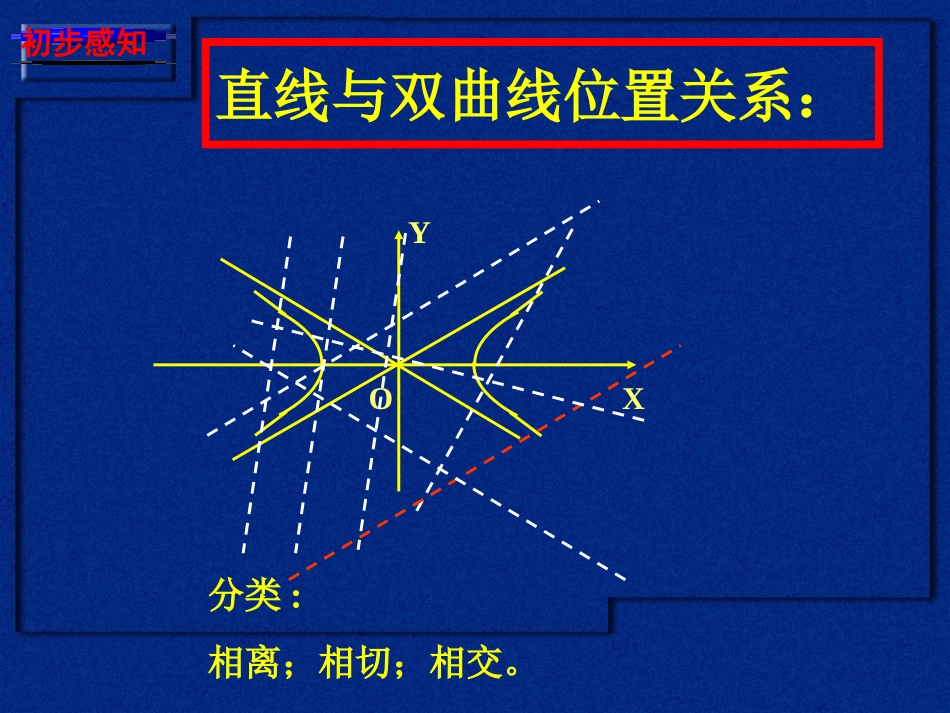
椭圆与直线的位置关系及判断方法判断方法∆<0∆=0∆>0（1）联立方程组（2）消去一个未知数（3）复习:相离相切相交直线与双曲线位置关系：XYO初步感知分类:相离；相切；相交。根据交点个数判定XYOXYO相离:0个交点相交:一个交点相交:两个交点相切:一个交点图象法:把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的渐近线平行相交（一个交点）计算判别式>0=0<0相交相切相离代数法:判断直线与双曲线位置关系的操作流程图例1.已知直线y=kx-1与双曲线x2-y2=4,试讨论实数k的取值范围,使直线与双曲线(1)没有公共点;(2)有两个公共点;(3)只有一个公共点;(4)交于异支两点；(5)与左支交于两点.(3)k=±1，或k=±；52(4)-1＜k＜1；(1)k＜或k＞；525252(2)＜k＜；52125-k1k且典型例题:221-kx+2kx-5=02.过原点与双曲线交于两点的直线斜率的取值范围是13422yx323，，2练习:BA例2过双曲线的右焦点作倾斜角为30°的直线，交双曲线于A、B两点，求|AB|.22136xyF1oF2xy163||5AB=典型例题:例3.以P（1，8）为中点作双曲线为y2-4x2=4的一条弦AB，求直线AB的方程。典型例题:解法一：（1）当过P点的直线AB和x轴垂直时，直线被双曲线截得的弦的中点不是P点。（2）当过P点的直线AB和x轴不垂直时，设其斜率为k。则直线AB的方程为y-8=k（x-1）22222y-8=kx-1由,得y-4x=4k-4x+2kk-8x+8-k-4=0112212,,,,,1AxyBxyxx设则是方程的两个不等实根.1222k-4x+2kk-8x+8-k-4=02222∴Δ=4k8-k-4k-48-k-4>021,8,ABP弦的中点是2k8-k∵中点坐标公式与韦达定理,得-=13k-422由13得k=12x直线AB的方程为y-81=即直线AB的方程为x-2y+15=0典型例题:112222112222,,,,44,44AxyBxyxx解法二:设则yy111112124,yyyyxxxx1,8,ABP弦的中点是12122,16.xxyy1112168,yyxx11121,2yyABxx直线的斜率为12x直线AB的方程为y-81=即直线AB的方程为x-2y+15=0典型例题:例4设两动点A、B分别在双曲线的两条渐近线上滑动，且|AB|＝2，求线段AB的中点M的轨迹方程.2214xy-=oxyBAM22414xy+=1122212122,,2,,2222AyyByyAByyyy设则由得典型例题:22练习题:已知双曲线C:2x-y=2与点P1,2.1求过点P1,2的直线l的斜率k的取值范围,使l与C有一个交点?两个交点?没有交点?2是否存在过P的弦AB,使AB的中点为P?3若Q1,1,试判断以点Q为中点的弦是否存在?312;223.kk或存在直线y=x+1;不存在练习题:1.直线与双曲线位置的判定方法有几何法和代数法；2.中点弦问题可通过设出直线与双曲线的交点坐标，利用点在曲线上代点作差后结合韦达定理整体运算，使问题获解，但须注意检验直线与双曲线是否相交。小结：221.直线l:y=kx+1与双曲线C:2x-y=1右支交于不同的两点A,B1求实数k的取值范围;2是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.2.已知焦点在x轴上的双曲线C的两条渐近线经过坐标原点且互相垂直，又知C的一个焦点与点A1,2-1关于直线y=x-1对称.1求双曲线C的方程.2是否存在直线y=kx+b与双曲线C交于P,Q两点,使2PQ恰被点,1平分?33设直线y=mx+1与双曲线C的右支交于B,C两点,另一直线l经过M-2,0及CB的中点,求直线l在y轴上的截距t的取值范围.作业：1212y-y∴=2，即k=2x-x∴L方程为:y-1=2(x-1)ìïïïïÞÞíïïïïî222yx-=12x-4x+3=0△<02y-1=2(x-1)方程组无解，故满足条件的L不存在。作业：3课本组题22y.(B4)给定双曲线x-=1,过点P(1,1)2能否作直线L使L与所给双曲线交于两点A,B,且P是线段AB的中点?说明理由.