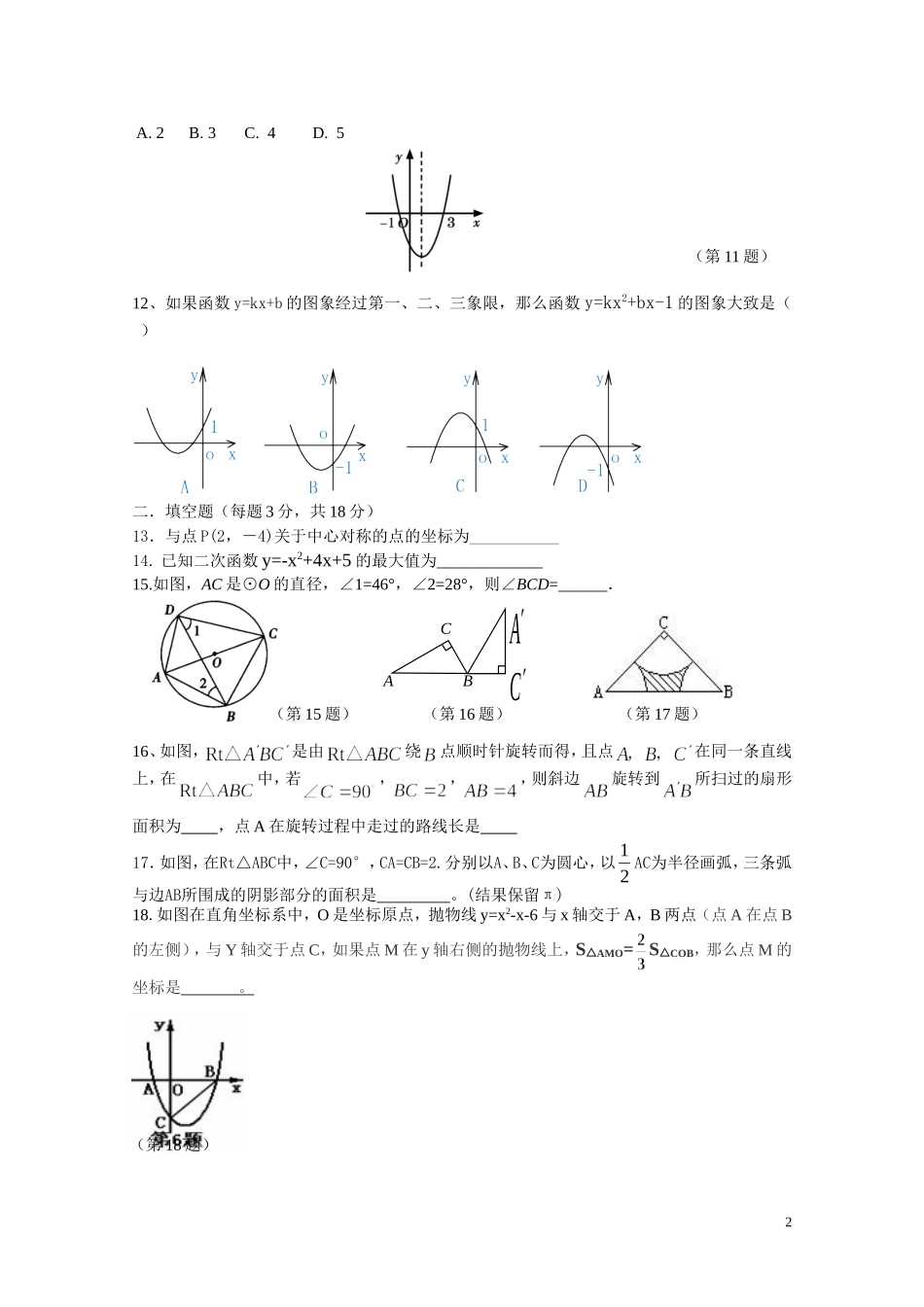
九年级数学第二次月考试题一.选择题(每题3分,共36分)1、下列事件中,是必然发生的事件的是()A、打开电视机,正在播放新闻B、父亲的年龄比儿子的年龄大C、通过长期努力学习,你会成为数学家D、下雨天,每个人都打着雨伞2.下列图案中,既是轴对称图形又是中心对称图形的是()3、下列图形中,旋转后可以和原图形重合的是()A、正六边形B、正五边形C、正方形D、正三角形4.过⊙O内一点M的最长的弦长为6厘米,最短的弦长为4厘米,则OM的长为()A.厘米B.厘米C.2厘米D.5厘米5.已知圆锥的底面半径是3,高是4,则这个圆锥侧面展开图的面积是()A.12πB.15πC.30πD.24π6、对于的图象下列叙述正确的是()A、顶点坐标为(-3,2)B、对称轴为y=3C、开口向下D、当x>3时随增大而增大7.有一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其它完全相同。小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是()A.6B.16C.18D.248.将抛物线y=5x2向左平移2个单位,再向下平移3个单位,得到的抛物线是()A.y=5(x+2)2+3B.y=5(x+2)2-3C.y=5(x-2)2+3D.y=5(x-2)2-39.已知二次函数y=2x2+8x+7的图象上有有点A,B,C,则y1、y2、y3的大小关系为()A.y1>y2>y3B.y2>y1>y3C.y2>y3>y1D.y3>y2>y110.已知⊙O的半径为1,点P到圆心O的距离为d,若关于x的方程x2-2x+d=0有实根,则点P().A.在⊙O的内部B.在⊙O的外部C.在⊙O上D.在⊙O上或⊙O的内部11、如图,为二次函数2yaxbxc的图象,给出下列说法:①0ab;②方程20axbxc的根为1213xx,;③0abc;④当1x时,y随x值的增大而增大⑤当0y时,13x.其中,正确的说法有个()1A.B.C.D.A.2B.3C.4D.512、如果函数y=kx+b的图象经过第一、二、三象限,那么函数y=kx2+bx-1的图象大致是()二.填空题(每题3分,共18分)13.与点P(2,-4)关于中心对称的点的坐标为___________14.已知二次函数y=-x2+4x+5的最大值为_____________15.如图,AC是⊙O的直径,∠1=46°,∠2=28°,则∠BCD=______.16、如图,是由绕点顺时针旋转而得,且点在同一条直线上,在中,若,,,则斜边旋转到所扫过的扇形面积为,点A在旋转过程中走过的路线长是17.如图,在Rt△ABC中,∠C=90°,CA=CB=2.分别以A、B、C为圆心,以21AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是。(结果保留π)18.如图在直角坐标系中,O是坐标原点,抛物线y=x2-x-6与x轴交于A,B两点(点A在点B的左侧),与Y轴交于点C,如果点M在y轴右侧的抛物线上,S△AMO=S△COB,那么点M的坐标是。2CBACA(第18题)(第17题)(第16题)(第15题)(第11题)19.(6分)解方程:20.(8分)如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.(1)画出四边形OABC关于y轴对称的四边形OA1B1C1,并写出点B1的坐标是.(2)画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2,并求出点C旋转到点C2经过的路径的长度.21.(6分)把二次函数(1)配方成y=a(x-h)2+k的形式,(2)求出它的图象的顶点坐标、对称轴。22.(8分)已知抛物线与x轴的交点是A(-1,0),B(2,0)且经过点C(3,8)。(1)求这个二次函数解析式,(2)求x为何值时,有最大(最小)值,这个值是什么?23、(8分)某商店进了一批服装,进货单价为50元,如果按每件60元出售可销售800件.如果每件升价1元出售,其销售量就减少20件.现在要获利1200元且销售成本部超过24000元.问这批服装销售单价定多少为宜?这时应进多少服装?24、(8分)某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).3商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元.(1)该顾客至少可得到元购物券,至多可得到元购物券;(2)请你用画树状图或列表的方法,求...