有理数的概念复习VIP免费

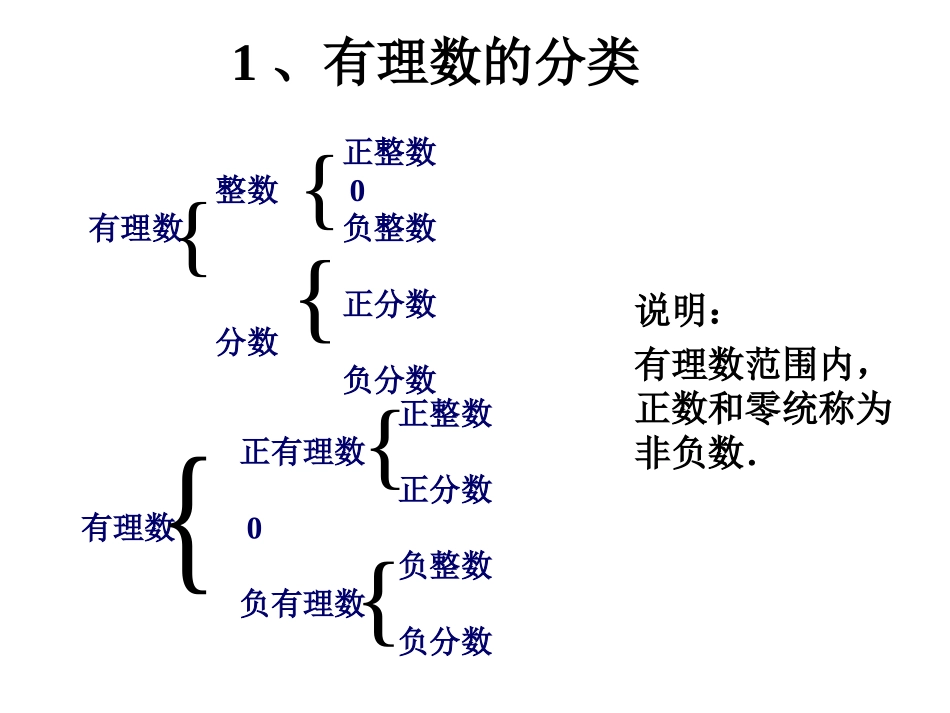
复习课有理数一、有理数的概念1、有理数的分类正整数整数0有理数负整数正分数分数负分数{正整数正有理数正分数有理数0负整数负有理数负分数{{{{{说明：有理数范围内，正数和零统称为非负数．练习1+7，-2，-8，，-3，0，+0.01，1正数集合：｛…｝；整数集合：｛…｝；正分数集合：｛…｝；负分数集合：｛…｝．3152212、数轴定义：规定了原点、正方向和单位长度的直线叫做数轴。在数轴上表示的两个数，右边的数总比左边的数大．练习21.在数轴上表示数的点：4，0，3，-15，-4，，2232.请说出下面的数轴上的点A、B、C各表示的数。ABC-2-1012-333、相反数定义：只有符号不同的两个数。a的相反数为-a4、绝对值1、几何定义：一个数a的绝对值就是数轴上表示a的点到原点的距离。2、代数定义一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0。字母说明：如果a＞0，那么|a|=a；如果a＜0，那么|a|=-a；如果a=0，那么|a|=0练习31、在括号里填写适当的数：=()；=()；-=()；-=()；2、讨论(1)绝对值是6的数有几个?各是什么?(2)绝对值是0的数有几个?各是什么?(3)有没有绝对值是-2的数?5.32153有理数的大小比较正数都大于0，负数都小于0。即负数＜0＜正数。数轴上两个点表示的数，右边的总比左边的大。两个负数，绝对值大的反而小。6.032:6.0326.06.0,3232::6.0__32::所以因为解比较大小例5、倒数定义：乘积为1的两个数互为倒数。结论：（1）0不能作除数，0没有倒数。（2）互为倒数的两个数符号相同。（3）倒数等于本身的数是+1，-1。1、一个数的绝对值是6.5，这个数＿＿。2、绝对值小于3的非负整数是＿＿＿＿。3、的相反数的倒数是＿＿＿＿＿。4、911_________,5,3baba则若练习45、先说出下列式子的意义，然后简化符号。（１）－（－７.３）（２）－（＋５）6、看谁水平高：（1）若–x=–6.3,则x=（）；若a=–72,则–a=（）；（2）若a+4=0，则a=（）.7、求下列各数的绝对值.-7.5+0.1-4.7510.58、如果|x|=2，求x的值。9、绝对值小于5的整数有哪些？10、化简（1）|-（+0.5）|（2）-|-13|11、比较大小（1）-1-0.01（2）-0.75-0.6512、|a+2|的最小值是____，此时a=_____。13、已知|a-3|+(b-2)2=0，则a=____,b=____。二、有理数的运算1、有理数的加法加法法则：1．同号两数相加，取相同的符号，并把绝对值相加；2．绝对值不相等的异号两数相加，取绝对值较大的加数符号，并用较大的绝对值减去较小的绝对值，互为相反数的两个数相加得0；3．一个数同0相加，仍得这个数．加法的运算律交换律：a+b=b+a．结合律：(a+b)+c=a+(b+c)2、有理数的减法减法法则：减去一个数，等于加上这个数的相反数．加、减法混合运算加减法统一成加法算式练习：1、把下面各式写成省略括号的和的形式：①10+(+4)+(-6)-(-5)；②(-8)-(+4)+(-7)-(+9)．2、说出式子8-7+4-6两种读法．练习6计算：（1）0.47－4－（－1.53）－1（2）（-４１）+（+２８）-（-５９）-（+７２）56163、有理数的乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘；任何数同0相乘，都得0．乘法运算律乘法交换律：ab=ba.乘法结合律：(ab)c=a(bc)．乘法分配律：a(b+c)=ab+ac.几个有理数相乘的积的符号法则1、几个不等于0的数相乘，积的符号由负因数的个数决定．当负因数有奇数个时，积为负；当负因数有偶数个时，积为正．2、几个有理数相乘，有一个因数为0，积就为0．4、有理数的除法法则：两数相除，同号得正，异号得负，并把绝对值相除．0除以任何一个不为0的数，都得0．除以一个不为0的数等于乘以这个数的倒数．练习71、计算：（1）(-4)×5×(-0.25)（2）2、用“＜”或“＞”号填空：（1）如果a＜0b＞0那么ab＿0（2）如果a＜0b＜0那么a÷b＿0)412(3)2(225、有理数的乘方幂的形式底数指数an乘方的符号法则1、正数的任何次幂都是正数；负数的奇次幂是负数，偶次幂是正数；零的任何次幂都是零．2、互为相反数的两个数的奇次幂仍互为相反数，偶次幂相等．3、任何一个数的偶次幂都是非负数．练习8计算：（1）（2）（3）543211322523102131111(...