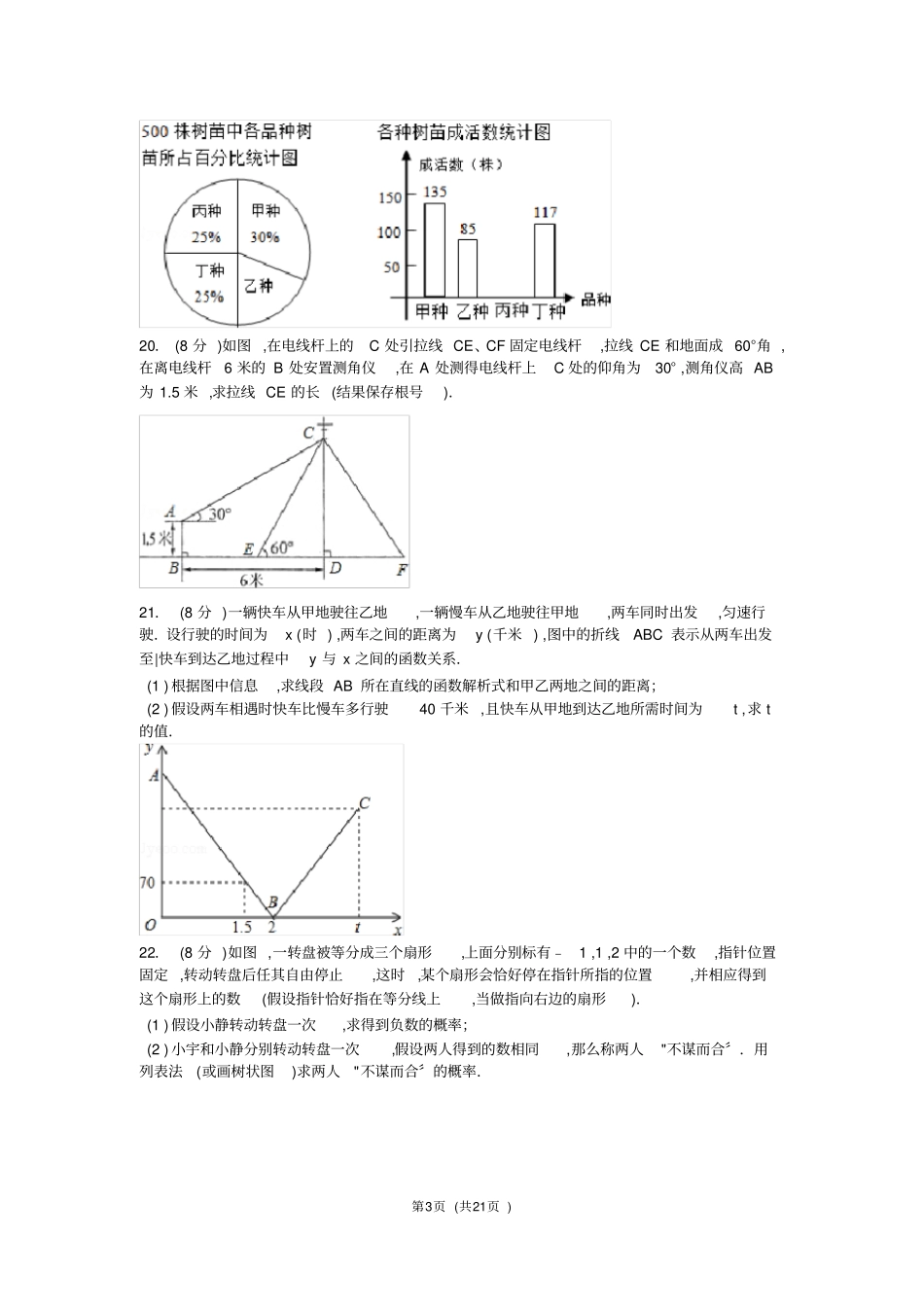
第1页(共21页)2021年陕西省中|考数学模拟试卷(一)一、选择题(每题3分,共30分.每题有四个答案,其中有且只有一个答案是正确.)1.(3分)|﹣0.5|的倒数是()A.0.5B.﹣2C.2D.2.(3分)以下计算中,正确的选项是()A.a3?a2=a5B.a3+a2=a5C.(a3)2=a9D.a3﹣a2=a53.(3分)如下图的几何体的左视图是()A.B.C.D.4.(3分)在物理学里面,光的速度约为8亿米/秒,该速度用科学记数法表示为()A.0.8×108B.8×106C.8×108D.8×1095.(3分)以下长度的三条线段能组成三角形的是()A.1,2,3B.3,4,8C.5,6,10D.5,6,116.(3分)一次函数y=kx+b(k≠0)经过(1,1)和(﹣2,3)两点,那么它的图象不过()A.第|一象限B.第二象限C.第三象限D.第四象限7.(3分)不等式2(x﹣2)≤x﹣2的非负整数解的个数为()A.1B.2C.3D.48.(3分)假设顺次连接四边形ABCD各边的中点所得四边形是矩形,那么四边形ABCD一定是()A.矩形B.菱形C.对角线互相垂直的四边形D.对角线相等的四边形9.(3分)如图,∠1=30°,∠B=60°,AB⊥AC,那么以下说法正确的选项是()A.AB∥CDB.AD∥BCC.AC⊥CDD.∠DAB+∠D=180°10.(3分)二次函数y=x2﹣2x﹣3的图象如下图.当y>0时,自变量x的取值范围是()第2页(共21页)A.﹣1<x<3B.x<﹣1C.x>3D.x<﹣1或x>3二、填空题(本大题共6小题,每题3分,总分值18分)11.(3分)计算2﹣|﹣2|=(结果保存根号)12.(3分)一元二次方程x2﹣6x+1=0的根为.13.(3分)请从以下两个小题中任选一个作答,假设多项选择,那么按所选的第|一题计分.A.一个扇形的弧长是20πcm,面积是120πcm2,那么这个扇形的圆心角是度.B.用科学计算器计算:cos21°=.(精确到0.01)14.(3分)一次函数y=x+b与反比例函数y=﹣有一个交点为(2,a),那么ba=.15.(3分)将抛物线y=x2﹣x向左平移1个单位,再向下平移2个单位,所得抛物线的解析式是.16.(3分)如图,第|一个图中两个正方形如下图放置,将第|一个图改变位置后得到第二个图,两图阴影局部的面积相等,那么该图可验证的一个初中数学公式为.三、解答题(共9小题,计72分.解容许写出过程)17.(5分)先化简,再求值:m﹣2()﹣(),其中m=,n=﹣1.18.(6分)如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.求证:(1)△ABE≌△CDF;(2)四边形BFDE是平行四边形.19.(7分)我市建设森林城市需要大量的树苗,某生态示范园负责对甲、乙、丙、丁四个品种的树苗共500株进行树苗成活率试验,从中选择成活率高的品种进行推广.通过实验得知:丙种树苗的成活率为89.6%,把实验数据绘制成下面两幅统计图(局部信息未给出).(1)实验所用的乙种树苗的数量是株.(2)求出丙种树苗的成活数,并把图2补充完整.(3)你认为应选哪种树苗进行推广?请通过计算说明理由.第3页(共21页)20.(8分)如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,测角仪高AB为1.5米,求拉线CE的长(结果保存根号).21.(8分)一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线ABC表示从两车出发至|快车到达乙地过程中y与x之间的函数关系.(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;(2)假设两车相遇时快车比慢车多行驶40千米,且快车从甲地到达乙地所需时间为t,求t的值.22.(8分)如图,一转盘被等分成三个扇形,上面分别标有﹣1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数(假设指针恰好指在等分线上,当做指向右边的扇形).(1)假设小静转动转盘一次,求得到负数的概率;(2)小宇和小静分别转动转盘一次,假设两人得到的数相同,那么称两人"不谋而合〞.用列表法(或画树状图)求两人"不谋而合〞的概率.第4页(共21页)23.(8分)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)求证:CD是⊙O的切线;(2)过点B作⊙O的切线交CD的延长线于点E,假设BC=6,tan∠CDA=,求BE的长.24.(10分)如图,抛物线经过A(4,0)、B(1,0)、C(0,﹣2)三点.(1)求此抛物线的解析式;(2)P是第|...