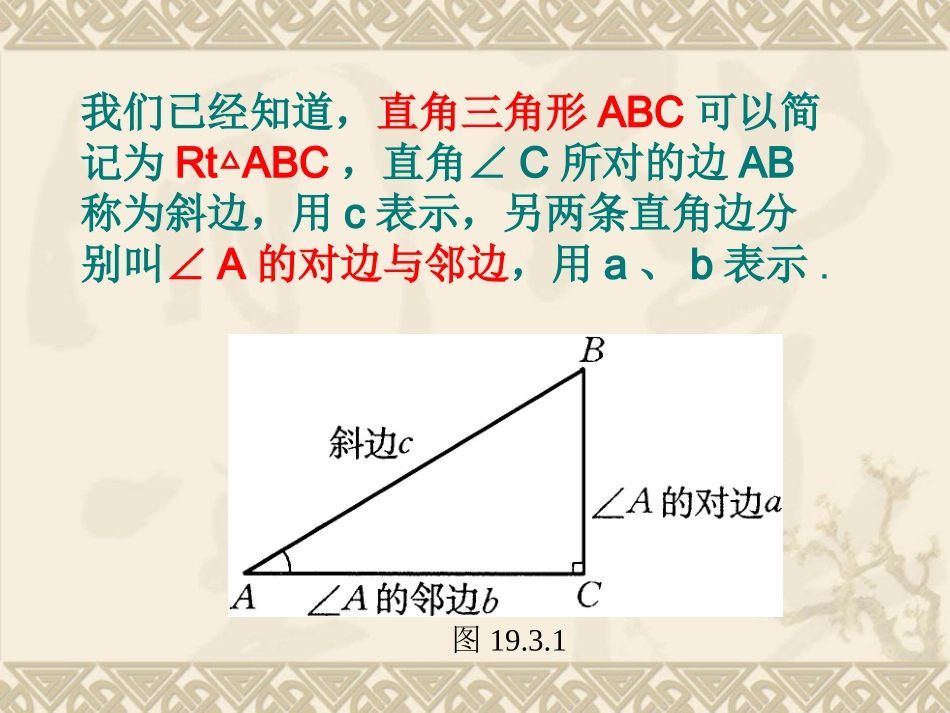
白鹤初中九年级数学组学习目标1、掌握锐角三角函数的定义2、能根据锐角三角函数进行正确计算我们已经知道,直角三角形ABC可以简记为RtABC△,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.图19.3.1如图,在RtMNP△中,∠N=90゜.P∠的对边是__________,P∠的邻边是_______________;∠M的对边是__________,M∠的邻边是_______________;(第1题)MNPNPNMN观察图19.3.2中的RtAB△1C1、RtAB△2C2和RtAB△3C3,它们之间有什么关系?图19.3.2RtAB△1C1RtAB∽△2C2RtAB∽△3C3所以=__________=__________.111ACCB可见,在RtABC△中,对于锐角A的每一个确定的值,其对边与邻边的比值是惟一确定的.B2C2AC2B3C3AC3图19.3.2想一想对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的吗?注意:1.1.我们研究的锐角三角函数都是在我们研究的锐角三角函数都是在直角三角形直角三角形中定义的中定义的..2.2.三角函数的实质是三角函数的实质是一个比值一个比值,没有单位,而且这个比值,没有单位,而且这个比值只与锐角的大小有关与三角形边长无关只与锐角的大小有关与三角形边长无关..3.3.sinA、cosA、tanA、cotA都是表达符号,它们是一个整体,不能拆开来理解.4.4.sinA、cosA、tanA、cotA中∠A的角的记号“∠”习惯省略不写,但对于用三个大写字母和阿拉伯数字表示的角,角的记号“∠”不能省略.如sin1∠不能写成sin1.理解定义:1、你认为∠A的正弦、余弦的定义有什么区别?正切、余切呢?2、你能利用直角三角形的三边关系得到sinA与cosA的取值范围吗?0<sinA<1,0<cosA<13、根据定义,sin2A和cos2A有什么关系?4、tanA与cotA之间有什么关系呢?tanA•cotA=1Sin2A+cos2A=1例1、求出图中所示的RtABC△中∠A的四个三角函数值.图19.3.1158变式:把上题的条件改成BC:AC=2:1,你能求出∠A的四个三角函数值吗?tanA=2例2已知,RtABC△中,∠C=900,sinA=,求sinB的值。32图19.3.1变式练习1、下图中∠ACB=90°,CDAB⊥指出∠A的对边、邻边。ABCD2、1题中如果BC=5,AC=10,则sin1=∠sin2=∠∟⌒⌒12510练一练1.判断对错:A10m6mBC1)如图(1)sinA=()(2)sinB=()(3)sinA=0.6m()(4)SinB=0.8()ABBCBCAB√√××sinA是一个比值(注意比的顺序),无单位;2)如图,sinA=()BCAB×小结通过我们这一节课的探索与学习,你一定有好多的收获,你能把这些知识点加以收集与总结吗?P91练习2、3作业