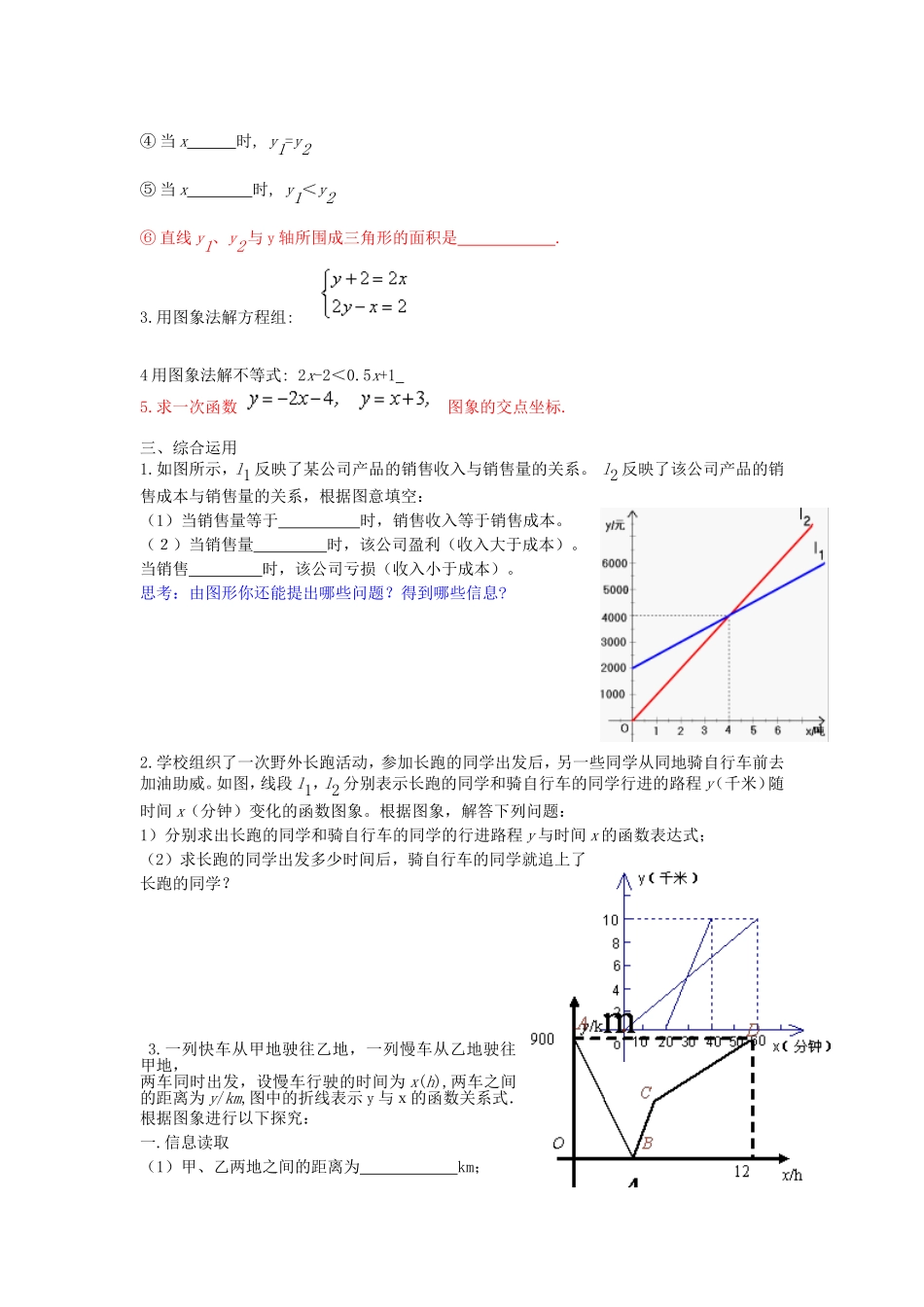
一次函数复习课教案主备人:杨化伟备课时间:教学目标:1.理解一元一次方程、一元一次不等式、二元一次方程组与一次函数之间的关系2.掌握怎样用函数图象解方程(组)或解不等式3.学会用函数思想解决问题,培养学生数学建模思想.4.渗透数形相结合思想.教学重点和难点重点:运用一次函数数形相结合思想解决实际问题难点:灵活运用数与形解决实际问题教学过程.一.复习回顾.1.一次函数的关系式是2.正比例函数的关系式是3.一次函数y=kx+b的图象是经过(0,)与(,0)的一条4.正比例函数y=kx的图象是经过(0,)与(1,)的一条.5.k,b与一次函数y=kx+b的图象与性质:k决定函数的增减性;b决定图象与y轴的交点位置②当k>0时,y随着x的增大而增大,③当k<0时,y随着x的增大而增大,④当b>0时,直线交于y轴的正半轴,⑤当b<0时,直线交于y轴的负半轴⑥当b=0时,直线交经过原点,二.简单应用1.一次函数y=kx+b的图象与x轴交于点(1,0);(-2,0)①方程kx+b=0的解是②则不等式kx+b>0的解集是③则不等式kx+b<0的解集是④此时一次函数的关系式是⑤△OAB的面积是⑥若将此图象向平移个单位,使直线经过原点,此时是函数.2.在同一坐标系中作一次函数y1=2x-2与y2=0.5x+1的图象.①求出它们和交点坐标是②则方程组的解是.③当x时,y1>y2④当x时,y1=y2⑤当x时,y1<y2⑥直线y1、y2与y轴所围成三角形的面积是.3.用图象法解方程组:4用图象法解不等式:2x-2<0.5x+15.求一次函数图象的交点坐标.三、综合运用1.如图所示,l1反映了某公司产品的销售收入与销售量的关系。l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(1)当销售量等于时,销售收入等于销售成本。(2)当销售量时,该公司盈利(收入大于成本)。当销售时,该公司亏损(收入小于成本)。思考:由图形你还能提出哪些问题?得到哪些信息?2.学校组织了一次野外长跑活动,参加长跑的同学出发后,另一些同学从同地骑自行车前去加油助威。如图,线段l1,l2分别表示长跑的同学和骑自行车的同学行进的路程y(千米)随时间x(分钟)变化的函数图象。根据图象,解答下列问题:1)分别求出长跑的同学和骑自行车的同学的行进路程y与时间x的函数表达式;(2)求长跑的同学出发多少时间后,骑自行车的同学就追上了长跑的同学?3.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y/km,图中的折线表示y与x的函数关系式.根据图象进行以下探究:一.信息读取(1)甲、乙两地之间的距离为km;(2)请解释图中B点的实际意义.图象理解(3)求慢车和快车的速度;(4)求线段BC所表示的y与x之间的函数关系式.并写出自变量的取值范围.问题解决(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?