空间两直线的位置关系VIP免费

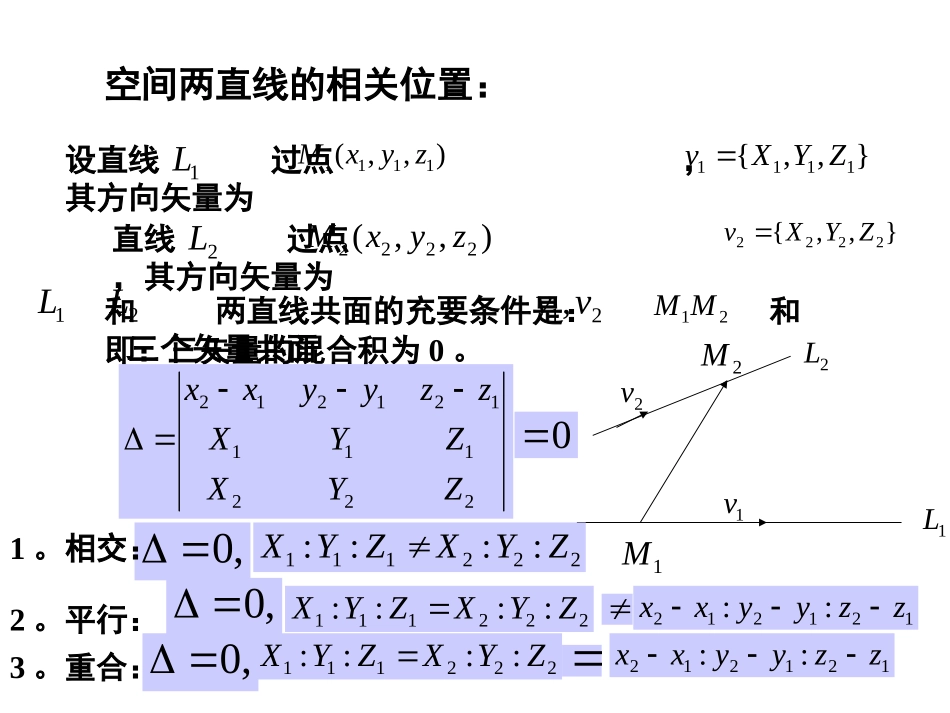
3.6空间两直线的相关位置1L2L1M2M1v2v空间两直线的相关位置：设直线过点，其方向矢量为1L},,{1111ZYXv直线过点，其方向矢量为2L},,{2222ZYXv和两直线共面的充要条件是：和三个矢量共面21,vv21MM即：三矢量的混合积为0。),,(1111zyxM),,(2222zyxM1L2L222111121212ZYXZYXzzyyxx0,0222111::::ZYXZYX1。相交：,0222111::::ZYXZYX121212::zzyyxx3。重合：,0222111::::ZYXZYX121212::zzyyxx2。平行：4。两直线异面的充要条件是：两直线的夹角：),(),(),(212121vvvvLL或因此，在直角坐标糸中，22222221212121212121),(cosZYXZYXZZYYXXLL212121),(cosvvvvLL即：两直线垂直的充要条件是：0212121ZZYYXX0222111121212ZYXZYXzzyyxx2L1L1N2N1M2M0L1v2v两异面直线的距离显然，两相交或重合直线的距离为零。两平行直线的距离等于其中一直线上的任一点到另一直线的距离。与两异面直线都垂直相交的直线叫做两异面直线的公垂线。两异面直线的距离就等于它们的公垂线夹于两异面直线间线段的长。12120MMNNL射影1221MMvv射影212112)(vvvvMM空间两直线上点的最短距离叫做两条直线之间的距离。因此，两异面直线之间的距离21211212)(vvvvMMNNd222112221122211222111212121YXYXXZXZZYZYZYXZYXzzyyxx两直线的公垂线方程2L1L1N2N1M2M0L1v2v公垂线可以看作由过点，以为方位矢量的平面及过点，以为方位矢量的平面的交线。1M2M211,vvv0L212,vvv因此，公垂线的方程为：0L00221122112211222222221122112211111111YXYXXZXZZYZYZYXzzyyxxYXYXXZXZZYZYZYXzzyyxx例1。求通过点P（1，1，1）且与两直线431221:,321:21zyxLzyxL都相交的直线的方程。解：1L过，过)0,0,0(1M2L)3,2,1(2M设所求直线的方向矢量为v=(X,Y,Z),,},,{},3,2,1{},1,1,1{11共面ZYXvnPM共面},,{},4,1,2{},2,1,0{22ZYXvnPM由02020412210,0321111ZYXZYXZYXZYX即可得：X：Y：Z=0：1：2所求直线的方程为：211101zyx则p1M2M1L2Lv例2。已知两直线011111:,0111:21zyxLzyxL（1）证明：两直线为异面直线；（2）求两直线间的距离；（3）求两直线的公垂线方程。解：（1）,04011011)1(10101两直线异面（2）}0,1,1{}0,1,1{21vv)2,0,0{222212121200)(vvvvMMd224（3）将数据代入公垂线方程，02000111110200011)1(00zyxzyx即00yxyx它也可表示为：00yx这条公垂线的方程就是z轴。00221122112211222222221122112211111111YXYXXZXZZYZYZYXzzyyxxYXYXXZXZZYZYZYXzzyyxx得习题讲解P。1321。解：X轴的方程为：00zy002211DxADxA（*）（1）当不全为0，且21,AA02211DADA因此，方程（*）有唯一解，即x轴与已知直线相交。（2）当且不全为0，方程（*）为矛盾方程，无解。因此，x轴与已知直线平行。021AA21,DD（3）当=0，方程（*）为恒等式，方程（*）有无穷多解。因此，x轴与已知直线重合。2121DDAA将它代入已知直线的方程，得：此时方程组（*）中只有一个独立方程。P。1336。解：MOOMMOOMMOOM),(cos1ddccbbaa共线与MOOM即直线通过原点O。MMP。1339。（1）解：3993465zxxzxz642335342zyxyzxz直线1：直线2：直线2过点N（0，-3，-4），其方向矢量设所求直线的方向矢量为v,因v//,所以v={8,7,1},它与直线1的交点设为M（9，b，39）,注意到NM，共面，因此}6,2,3{2v2,vv0623178439309b解之，得92b因此，所求直线的方程为：13979289zyxMN2vvxyz1L2L0L0LoP。1339。（2）解：tztytxLtztytxL74105:,5332:21设所求直线L与的交点为P，它所对应的参数为L与的交点为Q，它...