ARMAARIMA模型介绍及案例分析VIP专享VIP免费

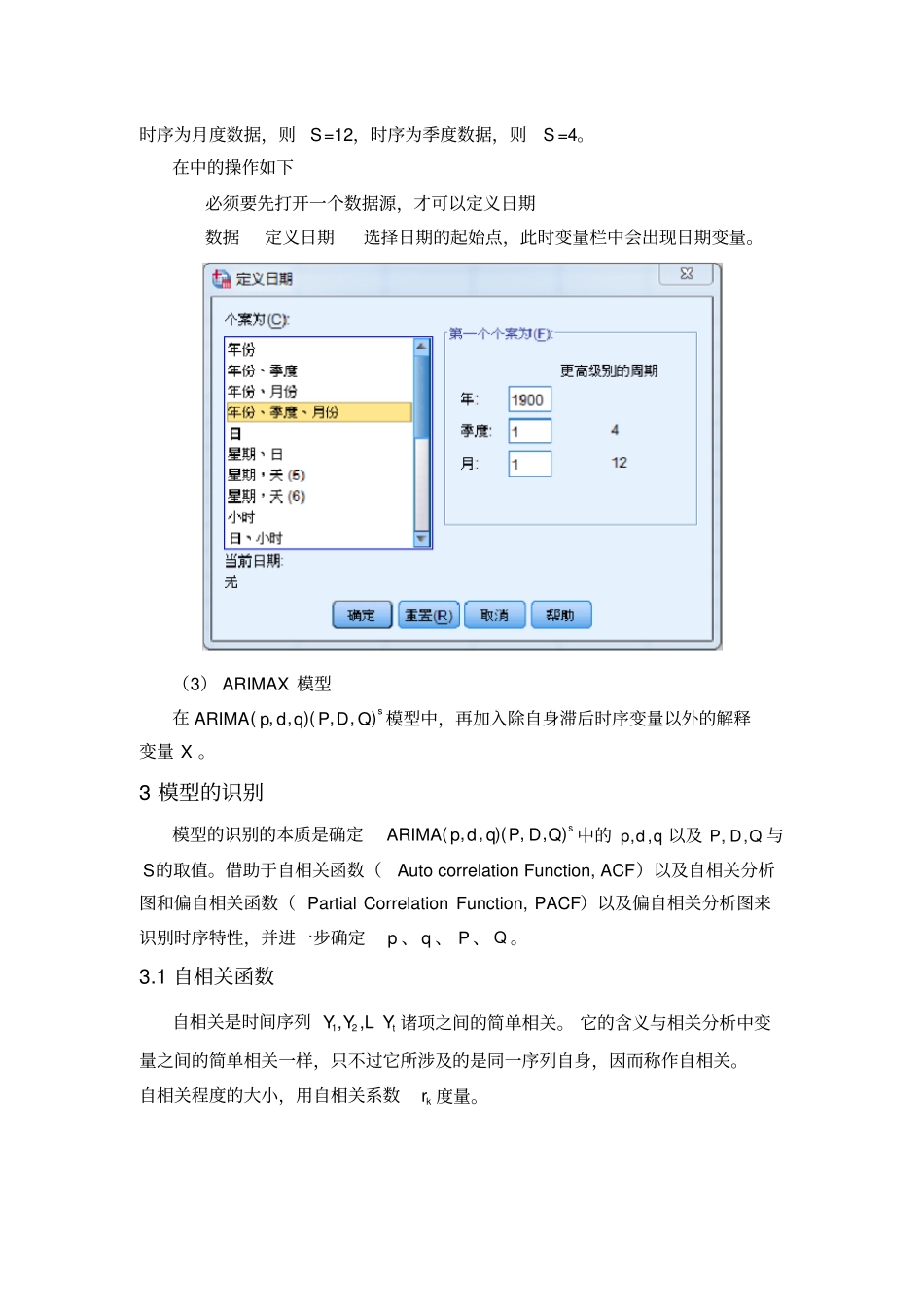
BOX-JENKINS预测法1适用于平稳时序的三种基本模型（1）()ARp模型（AutoregressionModel）——自回归模型p阶自回归模型：????=??+?1????-1+?2????-2+?+???????-??+????式中，????为时间序列第??时刻的观察值，即为因变量或称被解释变量；????-1，????-2，?，????-??为时序????的滞后序列，这里作为自变量或称为解释变量；????是随机误差项；??，?1，?2，?，???为待估的自回归参数。（2）()MAq模型（MovingAverageModel）——移动平均模型q阶移动平均模型：1122ttttqtqyeeeeL式中，为时间序列的平均数，但当{}ty序列在0上下变动时，显然=0，可删除此项；te，1te，2te，⋯，tqe为模型在第t期，第1t期，⋯，第tq期的误差；1，2，⋯，q为待估的移动平均参数。（3）(,)ARMApq模型——自回归移动平均模型（AutoregressionMovingAverageModel）模型的形式为：11221122tttptptttqtqycyyyeeeeLL显然，(,)ARMApq模型为自回归模型和移动平均模型的混合模型。当q=0,时，退化为纯自回归模型()ARp；当p=0时，退化为移动平均模型()MAq。2改进的ARMA模型（1）(,,)ARIMApdq模型这里的d是对原时序进行逐期差分的阶数，差分的目的是为了让某些非平稳（具有一定趋势的）序列变换为平稳的，通常来说d的取值一般为0,1,2。对于具有趋势性非平稳时序，不能直接建立ARMA模型，只能对经过平稳化处理，而后对新的平稳时序建立(,)ARMApq模型。这里的平文化处理可以是差分处理，也可以是对数变换，也可以是两者相结合，先对数变换再进行差分处理。（2）(,,)(,,)sARIMApdqPDQ模型对于具有季节性的非平稳时序（如冰箱的销售量，羽绒服的销售量），也同样需要进行季节差分，从而得到平稳时序。这里的D即为进行季节差分的阶数；,PQ分别是季节性自回归阶数和季节性移动平均阶数；S为季节周期的长度，如时序为月度数据，则S=12，时序为季度数据，则S=4。在中的操作如下必须要先打开一个数据源，才可以定义日期数据定义日期选择日期的起始点，此时变量栏中会出现日期变量。（3）ARIMAX模型在(,,)(,,)sARIMApdqPDQ模型中，再加入除自身滞后时序变量以外的解释变量X。3模型的识别模型的识别的本质是确定(,,)(,,)sARIMApdqPDQ中的,,pdq以及,,PDQ与S的取值。借助于自相关函数（AutocorrelationFunction,ACF）以及自相关分析图和偏自相关函数（PartialCorrelationFunction,PACF）以及偏自相关分析图来识别时序特性，并进一步确定p、q、P、Q。3.1自相关函数自相关是时间序列12,,tYYYL诸项之间的简单相关。它的含义与相关分析中变量之间的简单相关一样，只不过它所涉及的是同一序列自身，因而称作自相关。自相关程度的大小，用自相关系数kr度量。121()()()nkttktknttyyyyryy式中，n为样本数据的个数；k为滞后期；y为样本数据平均值。自相关系数kr，可看作自变量k的函数，即自相关函数。它表示时间序列滞后k个时间段的两项之间相关的程度。如1r表示每相邻两项间的相关程度；2r表示每隔一项的两个观察值得相关程度。随机序列自相关系数的抽样分布，近似于以0为均值，1n为标准差的正态分布。自相关系数的95%置信区间为(1.96,1.96)，此处1n。如果一个时间序列的自相关系数全部落入这个区间，则认为该序列是纯随机序列。将时间序列的自相关系数绘制成图，并标出一定的置信区间（通常采用2倍标准差作为置信区间的两个端点），被称作自相关分析图。中的操作1.输入变量数据；定义时间序列日期（数据定义日期）2.分析预测自相关（如下）；将要分析的变量从左侧移入右侧变量框中3.勾选自相关、偏自相关，转换暂时不选（如果为非平稳序列，可勾选差分/自然对数转换，其中差分的阶数需要根据自相关图形来确定，通常为0,1,2）未进行差分处理，由图可知几乎一半的自相关系数未进入置信区间，说明该序列非平稳，此时需要进行差分处理，即在重复第2步时，差分选项选择1或2。3.2偏自相关函数偏自相关函数是时间序列tY，在给定了121,,tttkYYYL的条件下，tY与tkY之间的条件相关。由于它需要考虑排除其他滞后期的效应，因而被称为偏自相关。偏自相关系数kk计算公式如下。111,111,112,3,1kkkjkjkkjkkjkjjrkrrkrL偏自相关系数kk，可看作自变量k的函数，...