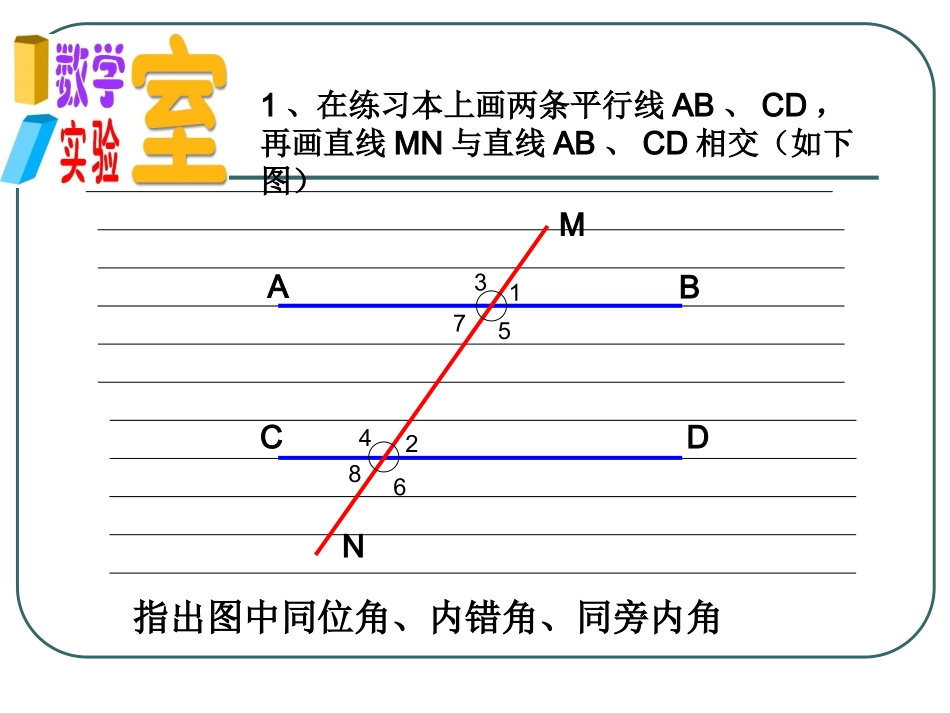
§7.2§7.2探索平行线的性质探索平行线的性质((一一))ABCDMN1、在练习本上画两条平行线AB、CD,再画直线MN与直线AB、CD相交(如下图)指出图中同位角、内错角、同旁内角751234682、将上图按照如下方式剪开,并分别把剪开得到的每对同位角、内错角重叠,你发现了什么?3、将图中的每对同旁内角剪成两部分,并把他们拼到一起去,你发现每对同旁内角之间有什么关系?做一做13527486结论两直线平行,同位角相等两直线平行,内错角相等两直线平行,同旁内角互补注意:只有在两直线平行的条件下才有:同位角、内错角相等,同旁内角互补。并不是所有的同位角、内错角都相等,同旁内角都互补如果我们现在只知道”两直线平行,同位角相等”.你能说明”两直线平行,内错角相等”成立的理由吗?如图∵ab(∥已知)∴∠1=2(∠两直线平行,同位角相等)又∵∠1=3(∠对顶角相等)∴∠2=3(∠等量代换)abc123请同学们仿照例子,把”两直线平行,同旁内角互补”的理由用几何语言表达出来.典例示范典例示范例如图,已知直线ab,∥∠1=500,求∠2的度数.abc12∴∠2=500(等量代换).解:∵ab(∥已知),∴∠1=2∠(两直线平行,内错角相等).又∵∠1=500(已知),变式1:已知条件不变,求∠变式1:已知条件不变,求∠33,∠,∠44的度数?的度数?34变式变式2:2:已知∠已知∠3=4∠3=4∠,∠,∠1=47°,1=47°,求∠求∠22的的度数?度数?∴∠2=470()解:∵∠∠3=4(∠3=4(∠))∴ab∥()又∵∠1=470()c1234abd如图:ADBC,A=C.∥∠∠试说明ABDC∥ABCFED解:ADBC(∵∥已知)∴∠C=CDE(∠两直线平行,内错角相等)又∵∠A=C(∠已知)∴∠A=CDE(∠等量代换)∴ABDC(∥同位角相等,两直线平行)小结(1)探索了平行线的性质(2)会运用直线平行的条件与性质解决简单的问题书第13页3、4