二次函数与一元二次方程第课时演示文稿VIP免费

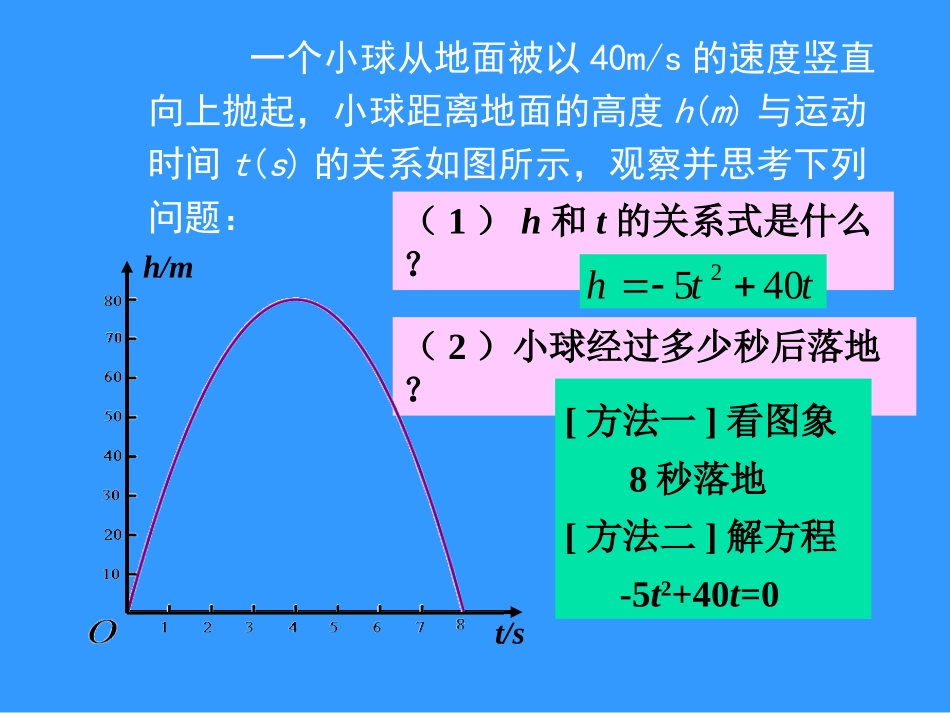
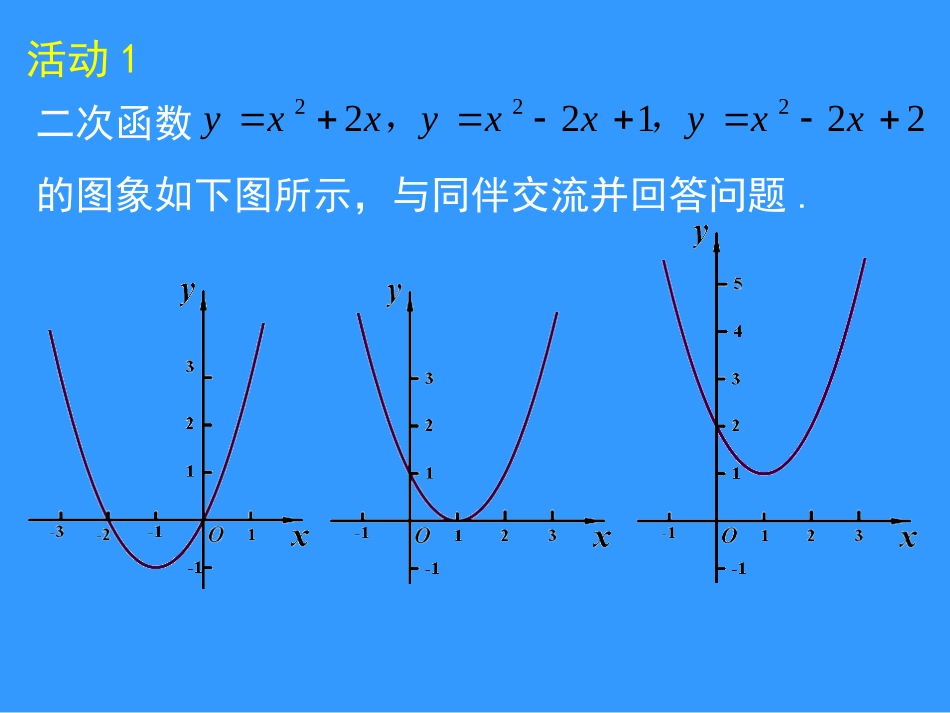
第二章二次函数2.5二次函数与一元二次方程（第1课时）（1）h和t的关系式是什么？tth4052（2）小球经过多少秒后落地？h/mt/s一个小球从地面被以40m/s的速度竖直向上抛起，小球距离地面的高度h(m)与运动时间t(s)的关系如图所示，观察并思考下列问题：[方法一]看图象8秒落地[方法二]解方程-5t2+40t=0二次函数的图象如下图所示，与同伴交流并回答问题.22122222xxyxxyxxy，，活动1二次函数的图象与x轴有几个交点？xxy22一元二次方程有几个根？022xx与x轴有两个交点：（-2,0）、（0,0）200200)2(21xxxxxx，或解：方程有两个根：0、-2二次函数的图象与x轴有几个交点？一元二次方程有几个根？122xxy0122xx与x轴有一个交点：(1,0)1010)1(212xxxx解：方程有两个相同的根：1二次函数的图象与x轴有几个交点？一元二次方程有几个根？222xxy0222xx与x轴没有交点方程没有实数根原方程无实数根解：04214)2(422acb议一议二次函数的图象与x轴的交点有三种情况：cbxaxy2一元二次方程ax2+bx+c=0的根有三种情况：有两个交点有一个交点没有交点有两个不相等的实数根有两个相等的实数根没有实数根二次函数的图象与x轴的交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系？cbxaxy2观察判断下列图象哪个有可能是抛物线的图象？yxOyxOyxOyxOA.B.C.D.322xxy√活动2观察函数的图象,完成填空：(1)抛物线与x轴有个交点，它们的横坐标是；(2)当x取交点的横坐标时，函数是；(3)所以方程的根是.22xxy022xx两-2，10x1=-2，x2=1观察函数的图象,完成填空：(1)抛物线与x轴有个交点，它们的横坐标是；(2)当x取交点的横坐标时，函数是；(3)所以方程的根是.442xxy0442xx一20x1=x2=2二次函数与x轴有交点，交点的横坐标为x0，那么当x=x0时，函数的值是0，因此x=x0就是方程的根.2yaxbxc20axbxc议一议二次函数的图象与x轴的交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系？cbxaxy2tth4052h/mt/s想一想（3）何时小球离地面的高度是60m？你是如何知道的？62062012860405602122tttttttth，令解))((:故2s和6s时，小球离地面的高度是60m.1.若方程的根为和，则二次函数的图象与x轴交点坐标是.2.二次函数的图象如图所示，则一元二次方程的解为.02cbxax21x32xcbxaxy2xxy22022xx一、课前检测，回顾迎新你能利用二次函数的图象估计一元二次方程的根吗？01022xx1.自主探索（1）观察二次函数的图象，抛物线与x轴的交点的横坐标约为_______.1022xxy二、合作交流，探索新知（2）由图象可知，方程有个根，一个根在和之间，另一个根在和（填两个整数）.01022xx（3）估计方程的近似根是（精确到0.1）01022xx2.小结反思（小组合作交流，解决问题）（1）用什么方法验证你的结果是否正确？（2）利用二次函数的图象求一元二次方程的近似根的一般步骤.3.及时强化试用二次函数的图象估计下列方程的近似根（1），（2）.2822xx11022xx1022xxy你是如何解决这一问题的，在小组内交流你们的解法.1.二次函数的图象如图所示，则一元二次方程的近似根是（精确到0.1）1422xxy01422xx三、运用提高，形成技能2.如图，已知抛物线的对称轴为，点A，B均在抛物线上，且AB与x轴平行，其中点A的坐标为（0,3），则点B的坐标为（）A.(2,3）B.(3,2）C.(3,3）D.(4,3）cbxxy22xOxyAx=2B3.利用二次函数的图象求一元二次方程的近似根.01522xx3.利用二次函数的图象求一元二次方程的近似根.01522xx谈谈你的收获和困惑[必做题]知识与技能1；数学理解2、3[选做题]数学理解4作业