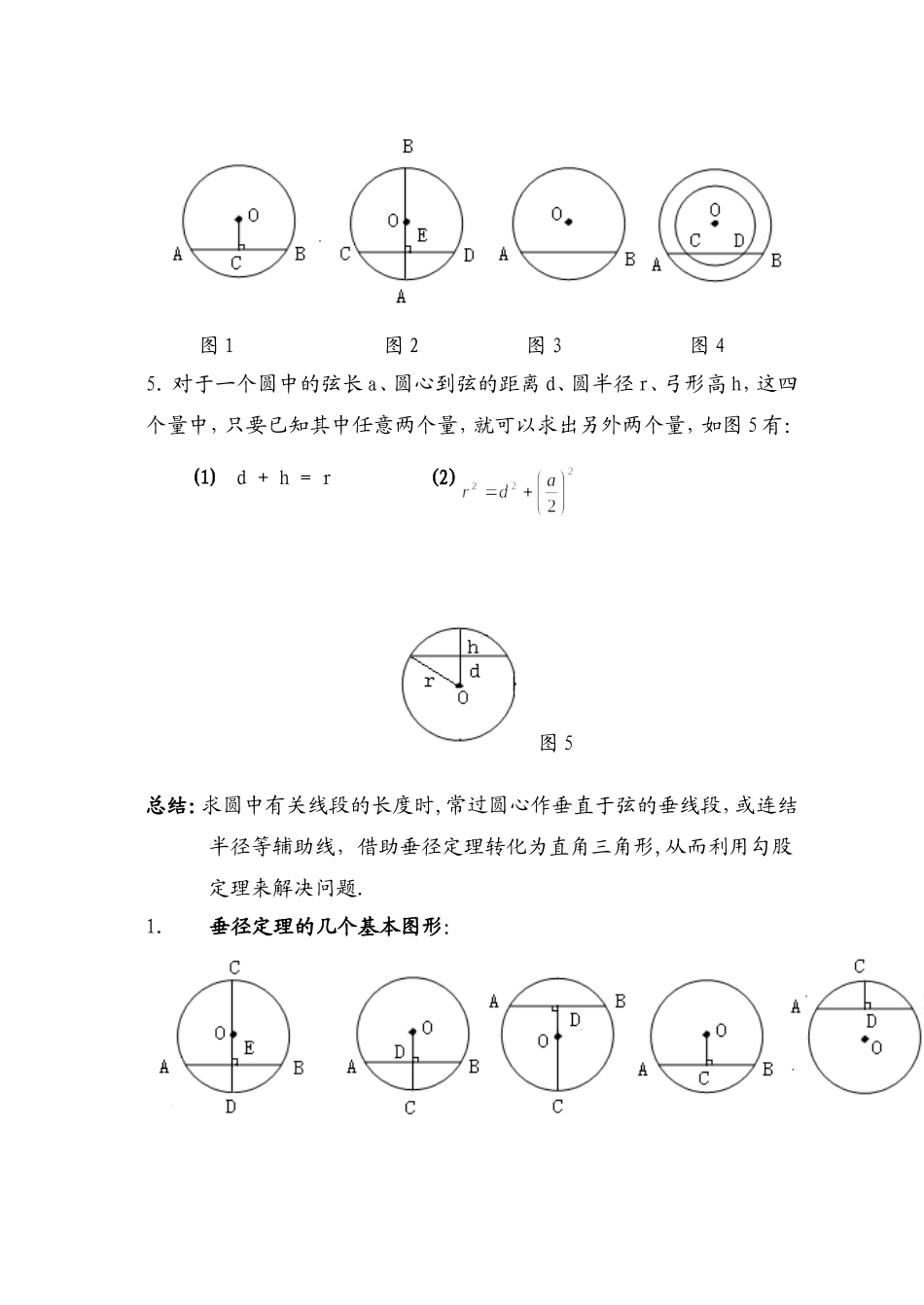
垂径定理及其应用一.复习引入1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.2.垂径定理的逆定理:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。几何语言:∵CD是直径,AM=BM∴CD⊥AB,AC=BC,AD=BD(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧.(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.二.新课讲解1.如图1,⊙O的半径为5,弦AB=8,OC⊥AB于C,则OC的长等于2、如图2,AB是⊙O的直径,弦CD⊥AB,垂足为E,若AB=10,CD=8,则AE的长为.3.如图3,在⊙O中,弦AB的长为8cm,若圆心O到AB的距离为3cm,则⊙O的半径为cm.4.如图4,同心圆O中,大圆的弦AB交小圆于点C、D,(1)请问AC=BD吗?(2)若两圆半径分别为5cm和cm,弦AB=8cm,则AC=cm.几何语言:∵CD是直径,CD⊥AB∴AM=BM,AC=BC,AD=BD图1图2图3图45.对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图5有:⑴d+h=r(2)图5总结:求圆中有关线段的长度时,常过圆心作垂直于弦的垂线段,或连结半径等辅助线,借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题.1.垂径定理的几个基本图形: