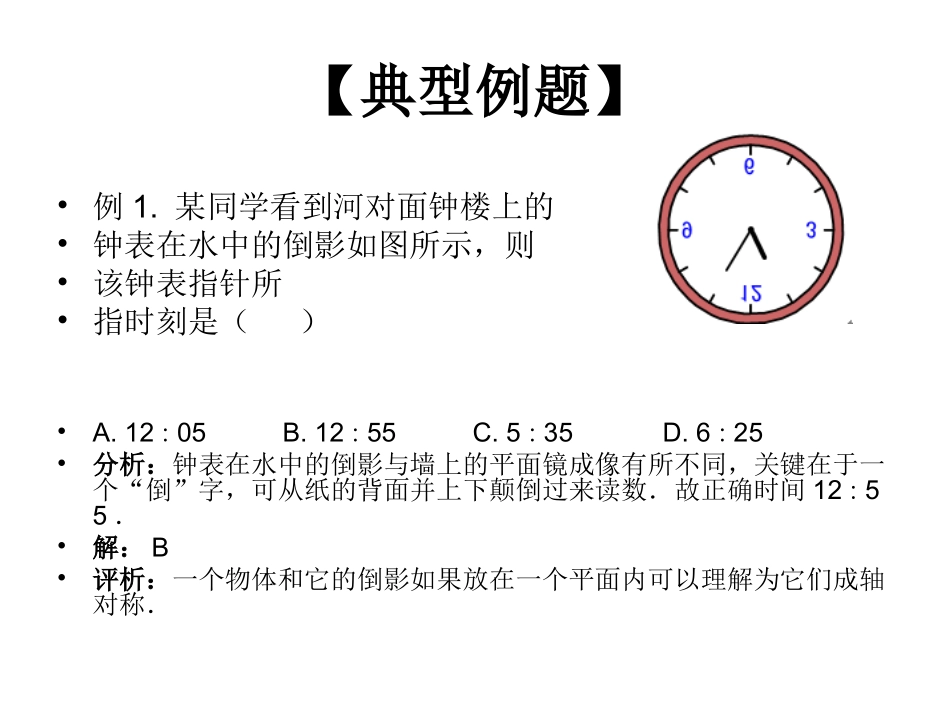
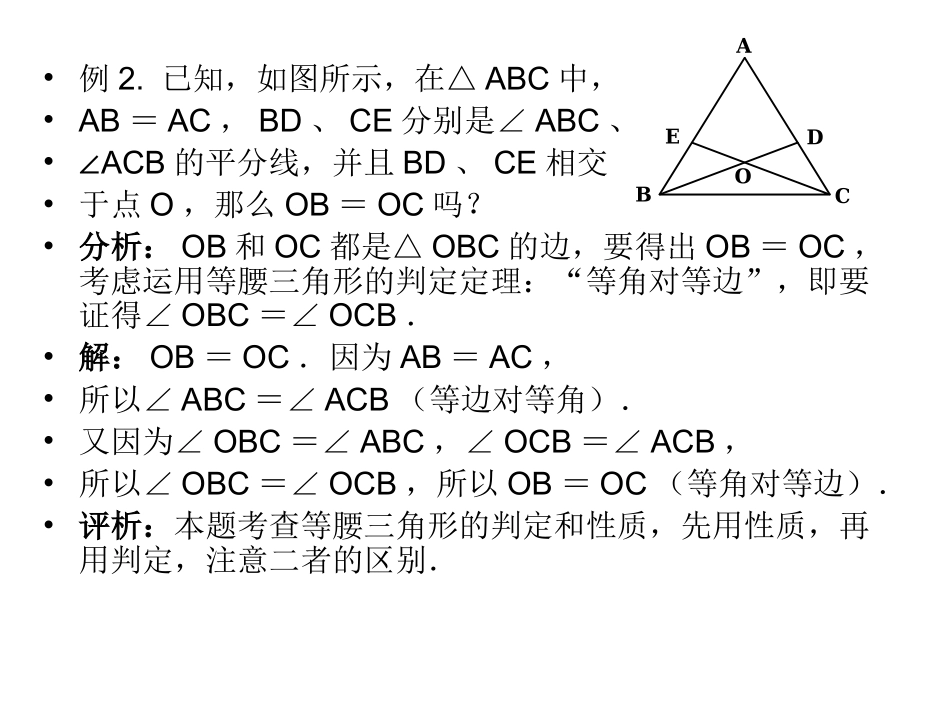
《轴对称综合复习》【典型例题】•例1.某同学看到河对面钟楼上的•钟表在水中的倒影如图所示,则•该钟表指针所•指时刻是()•A.1205∶B.1255∶C.535∶D.625∶•分析:钟表在水中的倒影与墙上的平面镜成像有所不同,关键在于一个“倒”字,可从纸的背面并上下颠倒过来读数.故正确时间125∶5.•解:B•评析:一个物体和它的倒影如果放在一个平面内可以理解为它们成轴对称.•例2.已知,如图所示,在△ABC中,•AB=AC,BD、CE分别是∠ABC、•∠ACB的平分线,并且BD、CE相交•于点O,那么OB=OC吗?•分析:OB和OC都是△OBC的边,要得出OB=OC,考虑运用等腰三角形的判定定理:“等角对等边”,即要证得∠OBC=∠OCB.•解:OB=OC.因为AB=AC,•所以∠ABC=∠ACB(等边对等角).•又因为∠OBC=∠ABC,∠OCB=∠ACB,•所以∠OBC=∠OCB,所以OB=OC(等角对等边).•评析:本题考查等腰三角形的判定和性质,先用性质,再用判定,注意二者的区别.ABCODE•例3.如图所示,已知在△ABC中,AB=AC,ADBC⊥于D且AD=BC=4,若将此三角形沿AD剪开成两个三角形,在平面上把这两个三角形拼成一个四边形,你能拼出所有的不同形状的四边形吗?画出所拼出的四边形的示意图(标出图中的直角).••分析:本题主要考查动手操作来探索答案,按照此题剪出所要求的两个三角形进行操作拼凑,分三种情况(斜边AB、直角边AD、直角边BD),不难得出四个符合要求的答案.•解:如图所示:••评析:拼接图形要考虑让哪两条边重合.ABCD剪开•例4.已知,如图所示,△ABC中,AB=AC,•∠BAC=120°,EF为AB的垂直平分线,•EF交BC于F,交AB于点E,•求证:FC=2BF.•分析:由AB=AC,∠BAC=120°,•易得∠B=∠C=30°,又已知EF是AB的垂直•平分线,联想到作辅助线,连结AF,得到AF=BF,•从而把问题FC=2BF转化为证FC=2AF.根据直角•三角形的知识,需证∠CAF=90°,问题得以解决.ABCEF•证明:连结AF,• EF为AB的垂直平分线•∴AF=BF,•∴∠B=∠FAB(等边对等角).• AB=AC,•∴∠B=∠C(等边对等角).• ∠BAC=120°,•∴∠B=∠C==30°(三角形内角和定理).•∴∠FAB=30°,•∴∠FAC=∠BAC-∠FAB=120°-30°=90°.•又 ∠C=30°,•∴FC=2AF(直角三角形中30°角所对的直角边等于斜边的一半).•∴FC=2BF.•评析:证明线段的2倍关系常常依赖于三角形的中线、直角三角形中30°角所对的直角•边等于斜边的一半等.注意到本题已知条件中有一个条件含120°,它与30°有密切的关系,所以解答本题的关键是把线段的2倍关系转化到一个含30°角的直角三角形中.•例5.(2008年新疆)在一次数学课上,王老师在黑板上画出下图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.要求同学从这四个等式中选出两个作为条件,推出△AED是等腰三角形.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)•已知:__________.•求证:△AED是等腰三角形.•分析:从四个等式中选出两个,有6种选法:①②,①③,①④,②③,②④,③④.验证这6种组合是不是能推出△AED是等腰三角形就可以了.另外,要注意本题有一个隐含相等关系,对顶角∠AEB=∠DEC.•解:已知:①③或①④或②③或②④,证明:△ABEDCE≌△.•以①③为例:•在△ABE和△DCE中,•∴△ABEDCE≌△,•∴AE=DE,即△AED是等腰三角形.•评析:本题是一道猜想型问题,又具有一定的开放性.考虑到从四个等式中选两个,共有六种选法,情况不太多,逐一验证就可以了.ABCDEABCDE•例6.已知△ABC为正三角形,点M是线段BC上任意一点,点N是线段CA上任意一点,且BM=CN,线段BN与AM相交于点Q.就下面给出的三种情况(如图①、②、③),先用量角器分别测量∠BQM的大小,然后猜测∠BQM等于多少度?并利用图③证明你的结论.••分析:图①和②区别不大,只是点M离B点远近不同,直接观察两个图形,发现△ABMBCN≌△,从而∠BAM=∠CBN,由外角知识∠BQM=∠BAM+∠ABN=∠ABC=60°.在图③中,图形稍显复杂,但是按照前面的思路,也应存在全等三角形△ABMBCN≌△,则∠BAM...