2.1.1-1根式根式.pptVIP免费

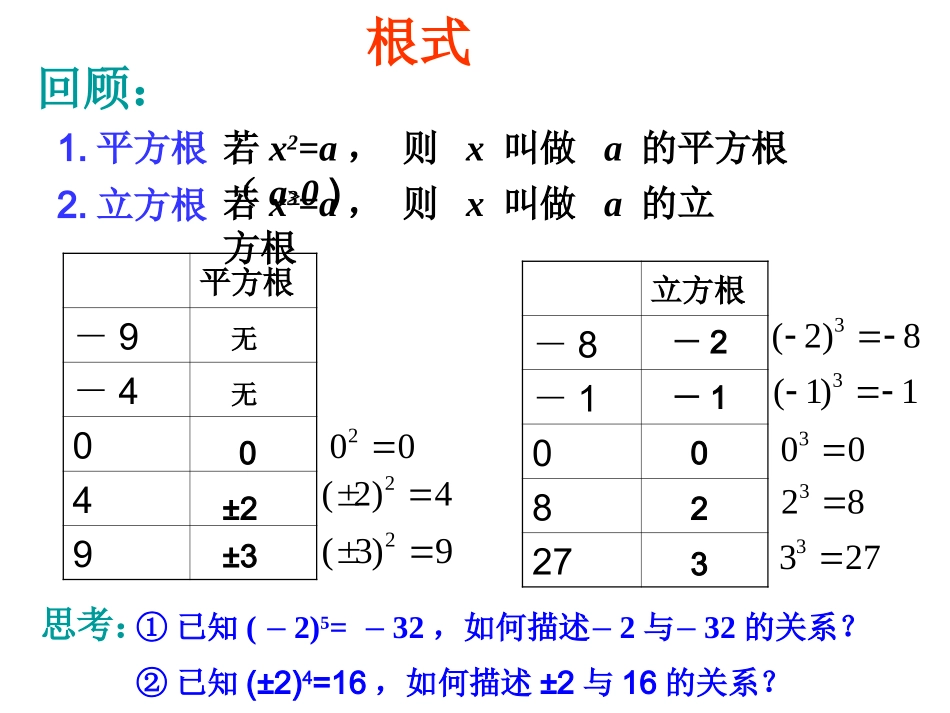
根式回顾：1.平方根若x2=a，则x叫做a的平方根（a≥0)2.立方根若x3=a，则x叫做a的立方根平方根－9－4049立方根－8－10827无无0±2±3－2－10232(2)42(3)92003(2)83(1)13003283327思考：①已知(－2)5=－32，如何描述－2与－32的关系？②已知(±2)4=16，如何描述±2与16的关系？定义1:①当n为奇数时,a的n次方根只有1个,用表示na②当n为偶数时,表示用)0(aan③0的任何次方根都是0若a<0,则a的n次方根不存在若a>0,则a的n次方根有2个,新知识点：.,1,,*Nnnnaxaxn且其中次方根的叫做那么若2(2)42(3)92003(2)83(1)13003283327定义1:①当n为奇数时,a的n次方根只有1个,用表示na②当n为偶数时,表示用)0(aan若a<0,则a的n次方根不存在若a>0,则a的n次方根有2个,新知识点：.,1,,*Nnnnaxaxn且其中次方根的叫做那么若练习：(1)25的平方根等于_________(2)27的立方根等于________(3)－32的五次方根等于_______(4)16的四次方根等于_______(5)a6的三次方根等于________(6)0的七次方根等于________±5－3－2±2a20③0的任何次方根都是0定义1:①当n为奇数时,a的n次方根只有1个,用表示na②当n为偶数时,表示用)0(aan若a<0,则a的n次方根不存在若a>0,则a的n次方根有2个,新知识点：.,1,,*Nnnnaxaxn且其中次方根的叫做那么若(当n是奇数);nax(当n是偶数,且a＞0).naxaxn即：③0的任何次方根都是0定义1:①当n为奇数时,a的n次方根只有1个,用表示na②当n为偶数时,表示用)0(aan若a<0,则a的n次方根不存在若a>0,则a的n次方根有2个,新知识点：.,1,,*Nnnnaxaxn且其中次方根的叫做那么若定义2:式子叫做根式,n叫做根指数,a叫做被开方数na(当n是奇数);nax(当n是偶数,且a＞0).naxaxn即：na根指数被开方数根式③0的任何次方根都是0定义2:式子叫做根式,n叫做根指数,a叫做被开方数na(当n是奇数);nax(当n是偶数,且a＞0).naxaxn即：例1:计算下列各式的值思考:①一定成立吗？nnaa②一定成立吗？nnaa①;22③;333②;2(2)④;33(3)44(1)⑤;①;24③;4416②;29④;331338⑤;4916－1－8232－31aann)(公式1：公式2：aann||aann当n为奇数时,当n为偶数时,0,0,aaaa①;22③;333②;2(2)④;33(3)44(1)⑤;①;24③;4416②;216④;331338⑤;4916－1－8232－31例2:求下列各式的值（式子中字母都大于零）323424(1)(8)(2)(10)(3)(3)(4)()()a-bab.510124(5)(0)(6)(0)aaaa(1)(2)(3)(4)练习:求下列各式的值:3-8;4(-2);2(2-3);441(3a-1)(a).3(5)526(6)423知识点小结：1、两个定义:——方根，根式2、两个公式：aann)(①aann||aann当n为奇数时,当n为偶数时,0,0,aaaa②补充：1.求下列各式的值：;)2()1(7744(3)(33);a343334(4)(8)(32)(23).作业：P59习题122412942025xxxx35,22x2.已知化简：;31)31()1(33xx.5)5()25)(5((2)2xxxx3.求出使下列各式成立的x的取值范围：(2)322322.