解直角三角形的应用(1)VIP免费

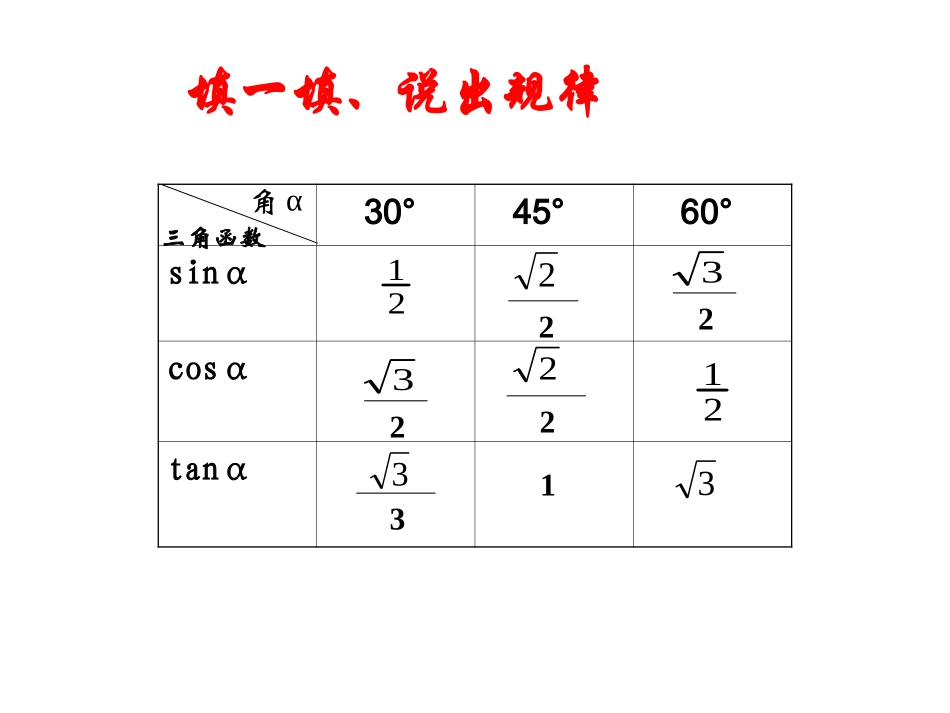
28.2.1解直角三角形30°45°60°sinαcosαtanα角α三角函数2122222132323133填一填、说出规律利用计算器可得.根据以上条件可以求出塔身中心线与垂直中心线的夹角．你能求出来吗？如图设塔顶中心点为B，塔身中心线与垂直中心线的夹角为A，过B点向垂直中心线引垂线，垂足为点C，在Rt△ABC中，∠C＝90°，BC＝5.2m，AB＝54.5mABC0954.05.542.5sinABBCAA528将上述问题推广到一般情形，就是：已知直角三角形的斜边和一条直角边，求它的锐角的度数.合作探究在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形.在直角三角形中除直角外，有五个元素，即有三条边和两个角.ABabcC（2）两锐角之间的关系∠A＋∠B＝90°（3）边角之间的关系caAA斜边的对边sincbBB斜边的对边sincbAA斜边的邻边coscaBB斜边的邻边cosbaAAA的邻边的对边tanabBBB的邻边的对边tan（1）三边之间的关系222cba（勾股定理）ABabcC在解直角三角形的过程中，一般要用到下面一些关系：在RtABC△中,想一想想一想不能不能ABC（2）根据∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?（1）根据∠A=60°，你能求出这个三角形的其他元素吗?（3）根据∠A=60°,斜边AB=4,你能求出这个三角形的其他元素吗?（4）根据BC=2，AC=2，你能求出这个三角形的其他元素吗？3∠BACBC∠A∠BAB在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.【例1】如图，在Rt△ABC中，∠C＝90°，解这个直角三角形.6,2BCACABC26BC6tanA3,AC2.3090.60ABA.222ACAB合作探究解:例2：在RtABC△中,C=90°,B=35°,b=20,∠∠解这个直角三角形.(精确到0.1)参考值tan35°≈0.70sin35°≈0.57cos35°≈0.82解:∵6.2870.02035tan20tantanBbaabB1.3557.02035sin20sinsinBbccbB尽量选择原始数据,避免累积错误∵5535909035BAB∴ABCab=c2035°1、在下列直角三角形中不能求解的是（）A、已知一直角边一锐角B、已知一斜边一锐角C、已知两边D、已知两角D练习巩固练习巩固ABCm2.如图，小明为了测量其所在位置，A点到河对岸B点之间的距离，沿着与AB垂直的方向走了m米，到达点C，测得∠ACB＝α，那么AB等于（）(A)m·sinα米(B)m·tanα米(C)m·cosα米(D)米tanmB3.边长为6cm的等边三角形中，其一边上高的长度为________cm.334、在RtABC△中,C=90∠°,已知，解这个直角三角形6,45cB1.拓展延伸2、如图,根据图中已知数据,求△ABC其余各边的长.ABC4503004cm总结梳理.归纳小结：解直角三角形的思路：(1)，明确已知什么，要求的元素有哪些；(2)，合理选择三角函数关系式，并正确进行变形（所选的关系式必须要有两个已知元素）；(3)，尽可能选用题目的原始数据，以减少误差.(4)，当图形中没有直角三角形时，要通过作辅助线构造直角三角形（作某边上的高是常用的辅助线）．作业：《广东中考》P144--145