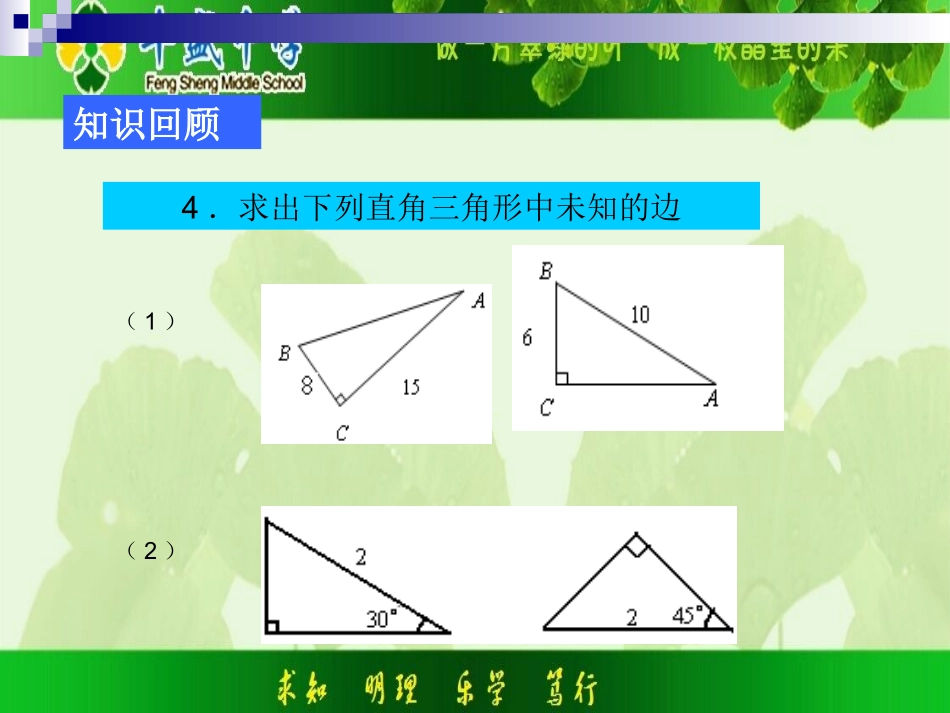
18.1勾股定理第4课时人教版初中数学八年级下册第十八章勾股定理知识回顾1.若c为RtABC△的斜边,b、a为直角边,则a、b、c的关系为___________.2.RtABC△的主要性质是:若∠C=90°,那么(用几何语言表示)⑴两锐角之间的关系:;⑵若∠B=30°,则∠B的对边和斜边,两直角边之间_________;若∠B=45°,则两直角边长,B∠的对边和斜边_________.a2+b2=c2∠A+B=90°∠的比为1:2的比为1:3相等的比为1:2知识回顾4.求出下列直角三角形中未知的边(2)(1)综合探究例1.在RtABC△中,∠C=90°.(1)已知:a=6,b=8,求c;(2)已知:a=40,c=41,求b;(3)已知:c=13,b=5,求a;(4)已知:a:b=3:4,c=15,求a、b.解:(1)(2)(3)(4)设a=3x,则b=4x,所以5x=15得x=3所以a=9,b=1222226810cab222241409bca222213512acb22229165cabxxx综合探究例2.如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?CBADE提示:①AD与BD有何关系?_____②设CD=x,则AD=,③在△ACD中根据勾股定理可列出构造方程来解.1.如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点D和点E,折痕DE的长为()A.1B.2C.1.5D.1.8EDBCA1题图矫正补偿2.如图所示,图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在RtABC△中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边向外延长一倍,得到图乙所示的“数学风车”,则这个风车外围周长(图乙中的实线)是__________.完善整合通过本节课的学习,我们复习了那些知识?1.本节课你又那些收获?2.复习时的疑难问题解决了吗?你还有那些疑惑?当堂测评1.如图,等腰△ABC中,AB=AC,AD是底边上的高,若AB=5cm,BC=6cm,则AD=cm.2.直角三角形两直角边长分别为3和4,则它斜边上的高为_______.3.某飞机在天空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每时飞行多少千米?第1题图第3题图作业布置必做题:课本第71页11题选做题:课本第71页12题