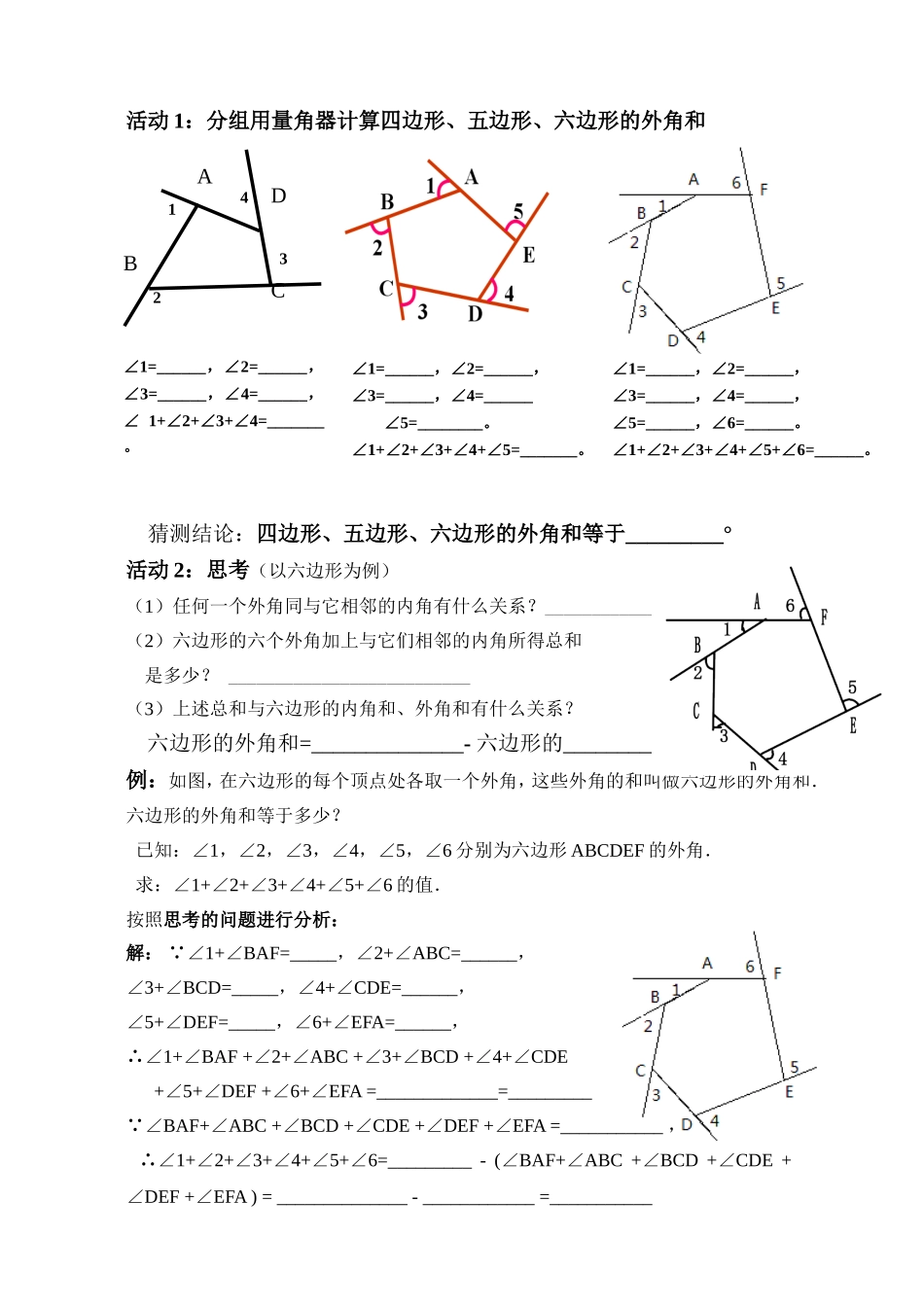
广州市第113中学学卷[课题]§11.3.2探索多边形的外角和班级:____________,姓名:_______________,日期:____________________[学习目标]1、掌握多边形的外角及外角和公式的推导;2、会用多边形内角和、外角和公式进行计算。3、经历探索多边形的外角和公式的过程.进一步发展的合情推理意识和说理能力,养成主动探究的习惯,同时培养善于发现、积极思考、合作学习、勇于创新的学习态度。学习过程]一、复习引入1、n边形内角和=__________;六边形的内角和为________;若一个多边形的内角和为1080°,多边形的边数是________。2、三角形的外角(和):(1)一个三角形共有______个外角,每个外角与其相邻内角之间的关系是___________。三角形的内角和等于_________,外角和等于__________。(2)课本书P75例2的另一种解法已知:如图,∠BAE、∠FBC、∠ACD是⊿ABC的外角。求:∠BAE、∠FBC、∠ACD的和。解法2: ∠1+∠BAE=_____°,∠2+∠FBC=_____°∠3+∠ACD=_____°∴∠1+∠BAE+∠2+∠FBC+∠3+∠ACD=_____________=_________ ∠1+∠2+∠3=________(______________________________),∴∠BAE+∠FBC+∠ACD=_______-(∠1+∠2+∠3)=__________=_______3、多边形的外角:多边形的一条边与它相邻的边的__________组成的角叫做多边形的________角。二、探索多边形的外角和1、多边形的外角和定义(同三角形外角和一样):多边形的外角和定义:在多边形的每个顶点处各取_______外角,这些外角的和叫做多边形的外角和.一般地,在多边形的每个顶点处按顺(逆)时针方向各取一个外角,n边形取n个外角.2、探究计算多边形的外角和ABCEF123DB活动1:分组用量角器计算四边形、五边形、六边形的外角和猜测结论:四边形、五边形、六边形的外角和等于_________°活动2:思考(以六边形为例)(1)任何一个外角同与它相邻的内角有什么关系?________________________(2)六边形的六个外角加上与它们相邻的内角所得总和是多少?__________________________(3)上述总和与六边形的内角和、外角和有什么关系?六边形的外角和=______________-六边形的__________例:如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?已知:∠1,∠2,∠3,∠4,∠5,∠6分别为六边形ABCDEF的外角.求:∠1+∠2+∠3+∠4+∠5+∠6的值.按照思考的问题进行分析:解: ∠1+∠BAF=_____,∠2+∠ABC=______,∠3+∠BCD=_____,∠4+∠CDE=______,∠5+∠DEF=_____,∠6+∠EFA=______,∴∠1+∠BAF+∠2+∠ABC+∠3+∠BCD+∠4+∠CDE+∠5+∠DEF+∠6+∠EFA=_____________=_________ ∠BAF+∠ABC+∠BCD+∠CDE+∠DEF+∠EFA=___________,∴∠1+∠2+∠3+∠4+∠5+∠6=_________-(∠BAF+∠ABC+∠BCD+∠CDE+∠DEF+∠EFA)=______________-____________=___________CABD3124∠1=______,∠2=______,∠3=______,∠4=______,∠5=______,∠6=______。∠1+∠2+∠3+∠4+∠5+∠6=______。∠1=______,∠2=______,∠3=______,∠4=______,∠1+∠2+∠3+∠4=_______。∠1=______,∠2=______,∠3=______,∠4=______∠5=________。∠1+∠2+∠3+∠4+∠5=_______。活动3:探究n边形的外角和如果把六边形改成n边形.(n为不小于3的正整数),同样也可以得到其外角和等于________°.即:结论:多边形的外角和等于_________°。所以我们说多边形的外角和与它的_______无关.计算过程:对此,我们也可以象以下这种,理解为什么多边形的外角和等于360°.如下图,从多边形的一个顶点A出发,沿多边形各边走过各顶点,再回到A点,然后转向出发时的方向,在行程中所转的各个角的和就是多边形的外角和,由于走了一周,所得的各个角的和等于一个_______,所以多边形的外角和等于_______°。三、例题学习例1:一个多边形的内角和等于它的外角和的3倍,它是几边形?例2.一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数。分析:正多边形的各个内角都相等,那么各个外角也都相等,而多边形的外角和是360°,因此只要求出每个外角度数,就可知是几边形了。四、课堂练习A组题1、多边形...