直线与双曲线的位置关系VIP免费

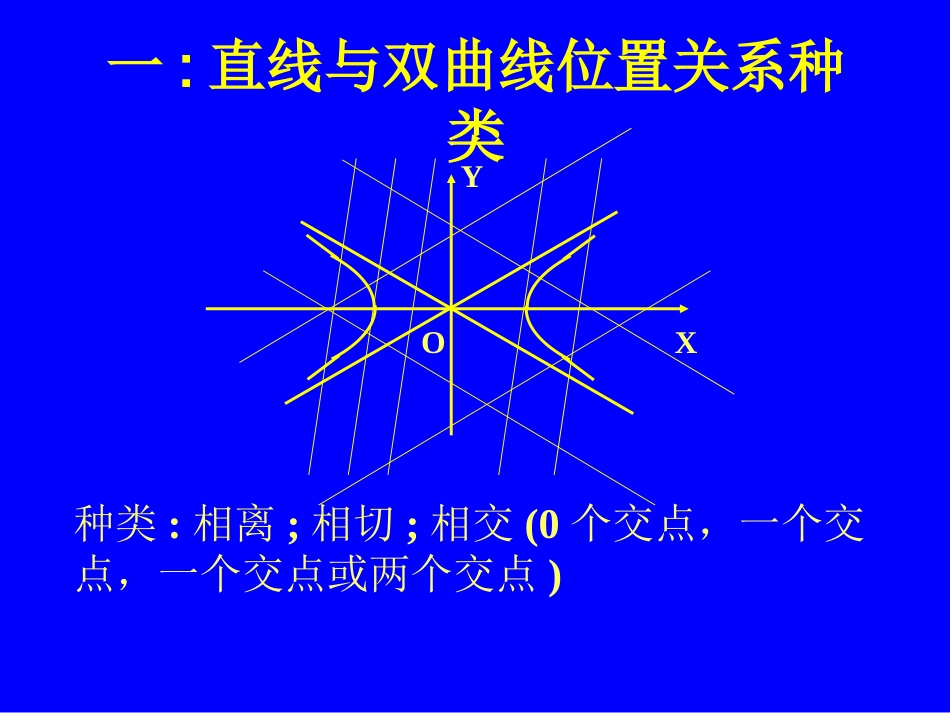
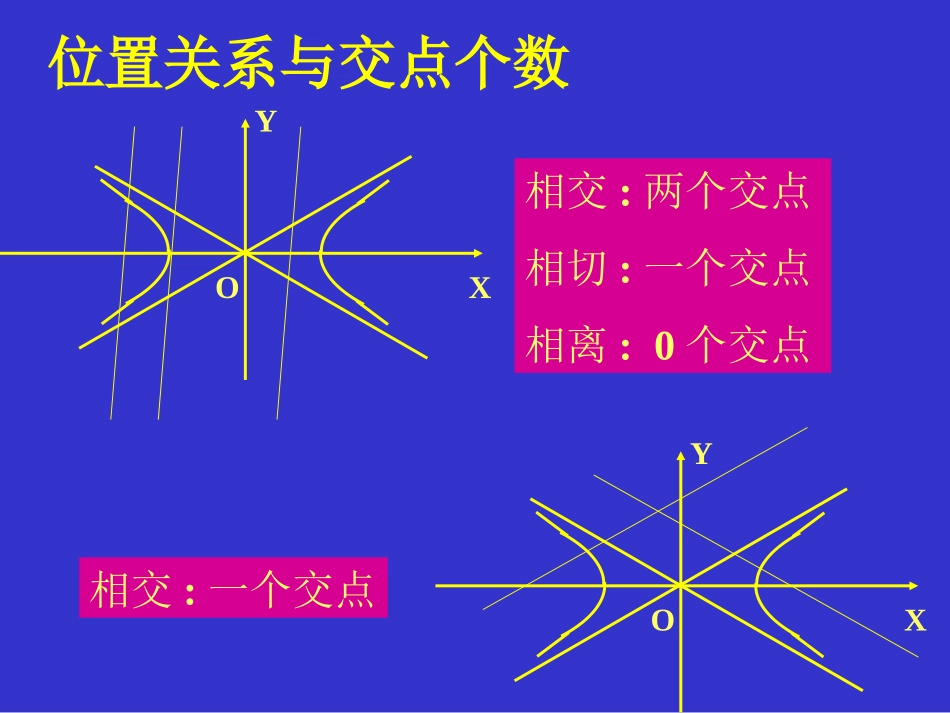
宜城三中官雄平一:直线与双曲线位置关系种类XYO种类:相离;相切;相交(0个交点，一个交点，一个交点或两个交点)位置关系与交点个数XYOXYO相交:两个交点相切:一个交点相离:0个交点相交:一个交点总结两个交点一个交点0个交点相交相切相交相离交点个数方程组解的个数有没有问题?天哪!=0一个交点?相切相交>0<00个交点两个交点相离相交[1]0个交点和两个交点的情况都正常,那么,依然可以用判别式判断位置关系[2]一个交点却包括了两种位置关系:相切和相交(特殊的相交),那么是否意味着判别式等于零时,即可能相切也可能相交?一般情况的研究1:,:2222byaxcmxabyl显然,这条直线与双曲线的渐进线是平行的,也就是相交.把直线方程代入双曲线方程,看看判别式如何?根本就没有判别式!唉!白担心一场!当直线与双曲线的渐进线平行时,把直线方程代入双曲线方程,得到的是一次方程,根本得不到一元二次方程,当然也就没有所谓的判别式了。结论：判别式依然可以判断直线与双曲线的位置关系！好也!=0一个交点相切>0<00个交点两个交点相离相交判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的渐进线平行相交（一个交点）计算判别式>0=0<0相交相切相离特别注意：直线与双曲线的位置关系中：一解不一定相切，相交不一定两解，两解不一定同支的方程。一个公共点，求直线仅有：与双曲线的直线过点lyxClP14223kxyl的方程为：设013641432222kxxkyxkxy由32:,2,0412xylkk此时时当313:,13,013446,042222xylkkkk此时得由时当4.3.2.1..14)0,2(22DCBAlyxClP条有线一个公共点，这样的直仅有：与双曲线的直线过点结合。解，故采用数形方程根的分布则不易求线方程，转化为此题为选择题，若设直003212011，、；，、；，、点的位置：改变PPPP例2.过点P(1,1)与双曲线只有共有_______条.变题:将点P(1,1)改为1.A(3,4)2.B(3,0)3.C(4,0)4.D(0,0).答案又是怎样的?4116922yx1.两条;2.三条;3.两条;4.零条.交点的一个直线XYO（1，1）。例2：设双曲线)0(1:222ayaxC与直线1:yxl相交于不同的点A、B，求双曲线C的离心率e的取值范围解：由题意知11222yxyax022)1(2222axaxa0)1(84012242aaaa120:aa且解得22611122eaaae且双曲线的离心率1axy例2：已知直线与双曲线1322yx交于A,B两点，若以AB为直径的圆过坐标原点，求实数a的值。