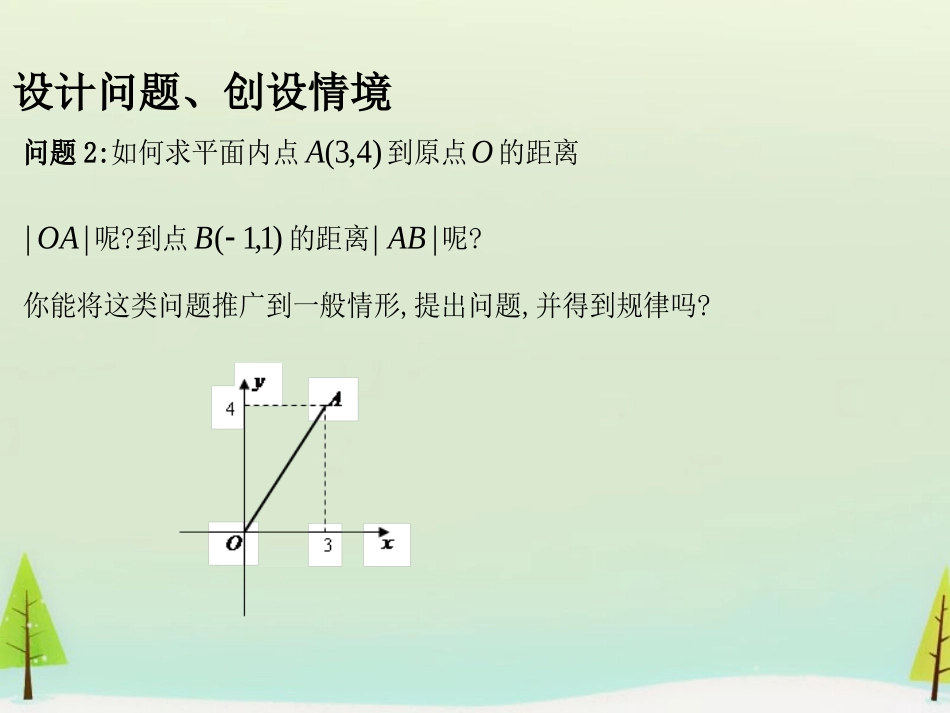
2.1.5两点间的距离设计问题、创设情境问题1:已知x轴上两点点)0,5(),0,1(BA,则两点BA,之间的距离||AB是多少?推广到一般情形,若x轴上两点点)0,(),0,(21xBxA,则两点BA,之间的距离||AB是多少呢?设计问题、创设情境问题2:如何求平面内点)4,3(A到原点O的距离||OA呢?到点)1,1(B的距离||AB呢?你能将这类问题推广到一般情形,提出问题,并得到规律吗?学生探索、尝试解决提出问题:已知平面上两点),(111yxP,),(222yxP,如何求21,PP的距离||21PP?问题3:大家是用什么办法求的||21PP?你是怎样想到构造直角三角形的?请大家交流一下.例题1.已知点)2,1(A,)7,2(B,在x轴上求一点P,使||||PBPA,并求||PA的值.运用规律、解决问题答案:)0,1(A,22||PA问题4:平面内要确定一个点,需要几个条件?求点的坐标这种题目,解答时可以考虑哪些方法?例题2:证明平行四边行四条边的平方和等于两条对角线的平方和.运用规律、解决问题坐标法解决平面几何问题的步骤第一步:建立直角坐标系,用坐标表示有关的量;第二步:进行有关代数运算;第三步:把代数结果“翻译”成几何关系.变练演编、深化提高变式训练:如图,ABD△和BCE△是在直线AC同侧的两个等边三角形,试证明AE=CD.信息交流、教学相长问题6:无论是距离公式的证明还是例1及例题2的求解,都体现了什么共同特征?上述过程必须借助什么来完成?反思小结、观点提炼通过本节课的学习,要求大家:(1)掌握平面内两点间距离公式及其推导过程;(2)能灵活运用此公式解决一些简单问题;(3)掌握如何建立适当的坐标系来解决几何问题,即坐标法的简单应用.