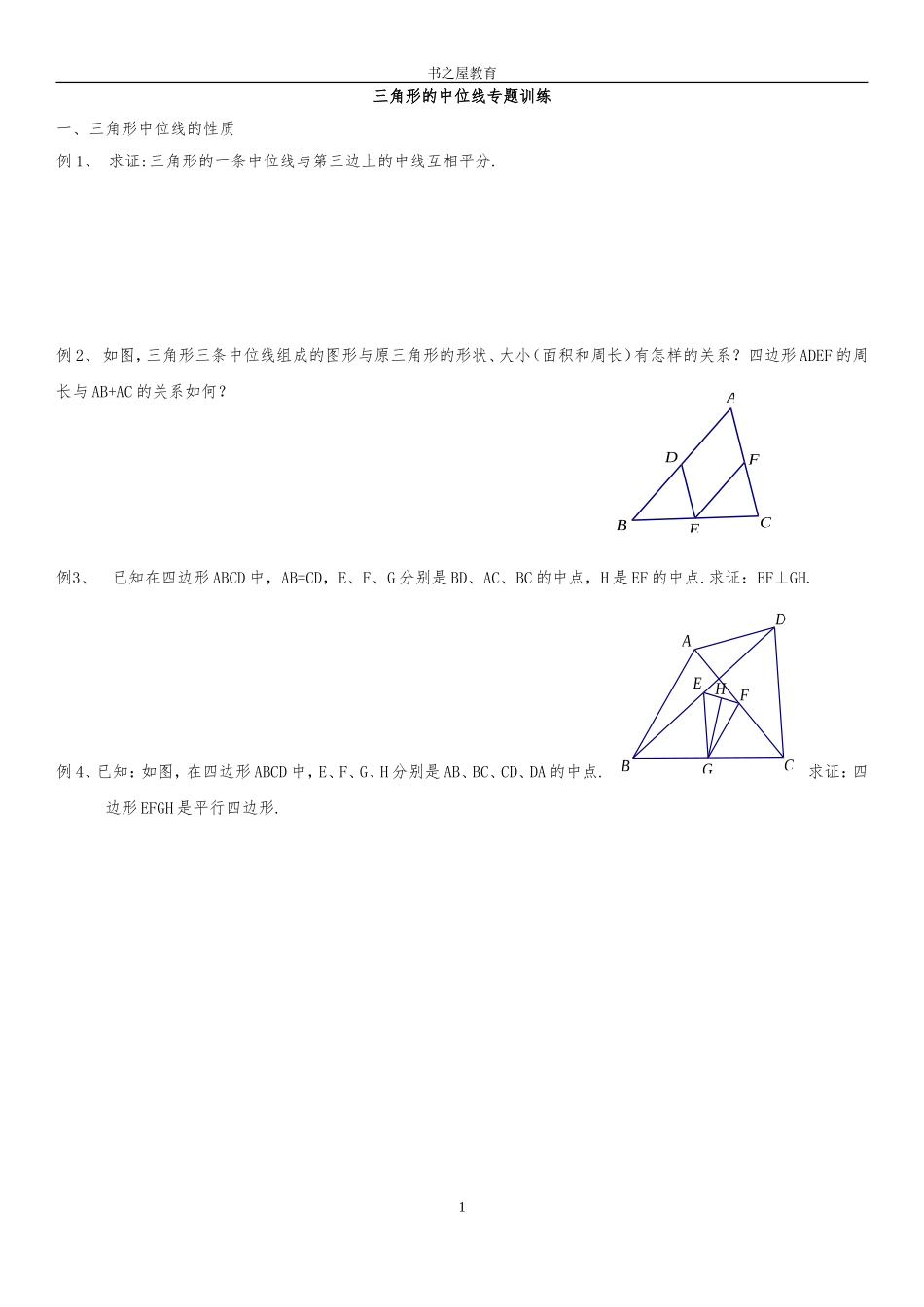
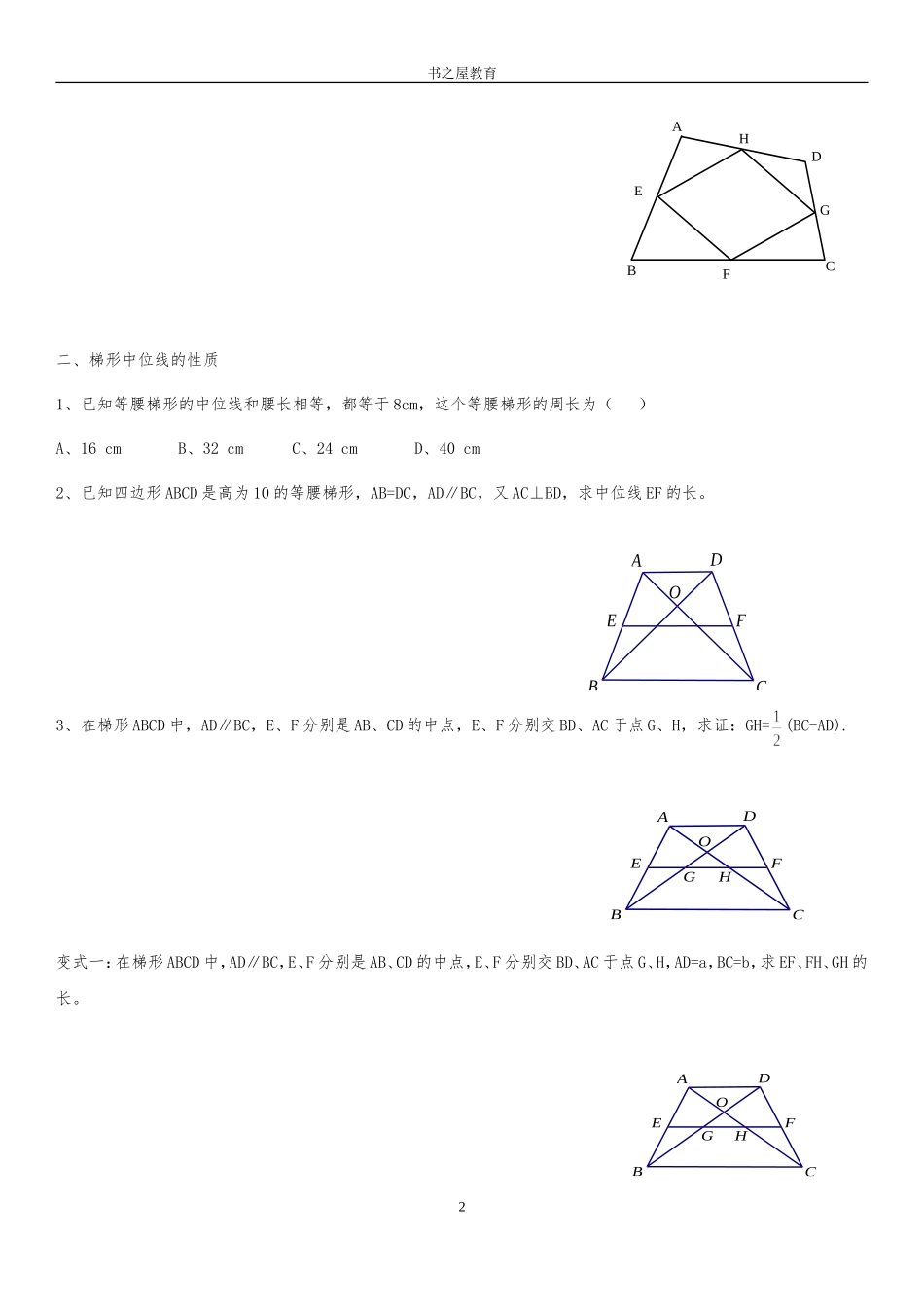
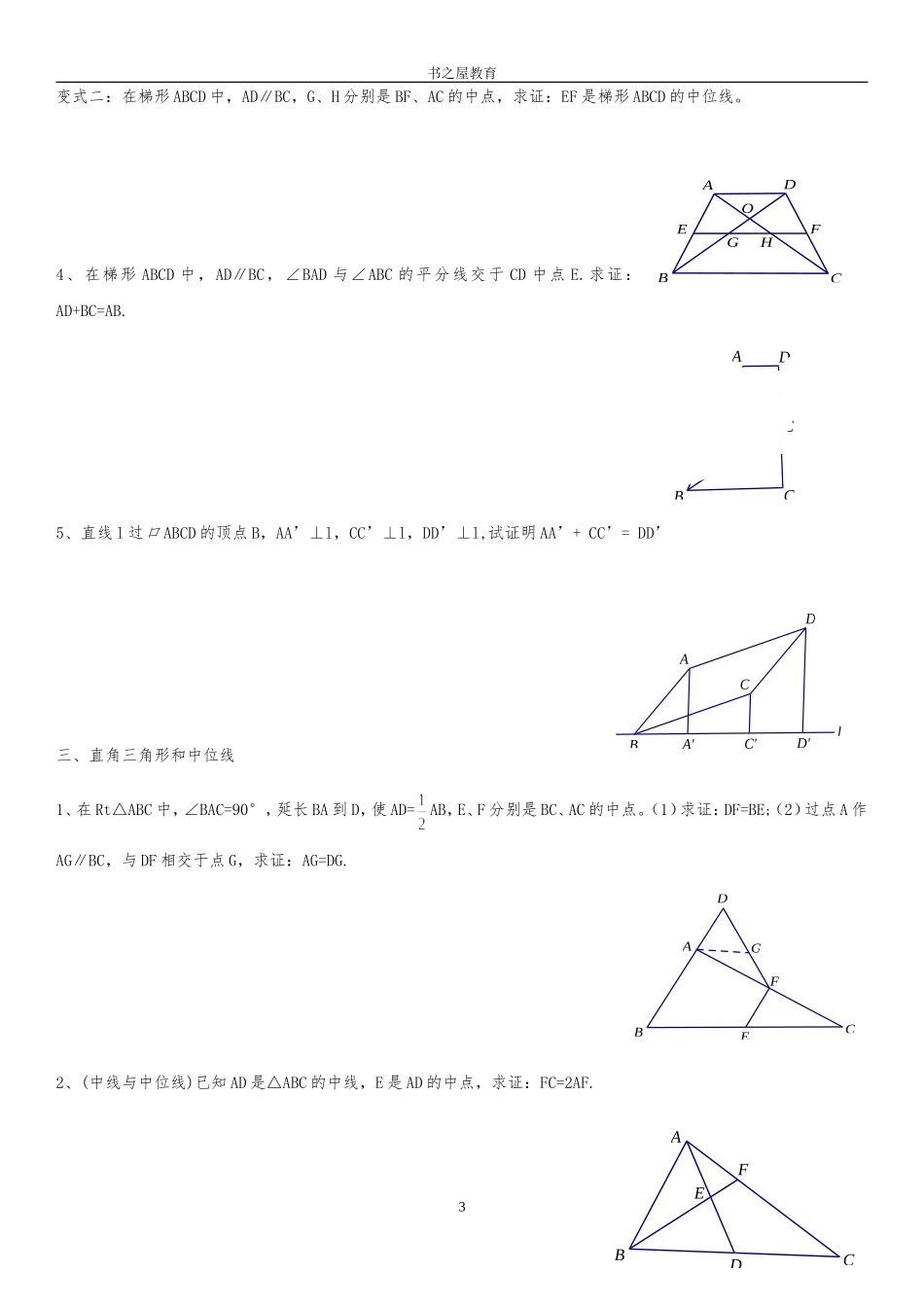
EFDABCHGEFDBAC书之屋教育三角形的中位线专题训练一、三角形中位线的性质例1、求证:三角形的一条中位线与第三边上的中线互相平分.例2、如图,三角形三条中位线组成的图形与原三角形的形状、大小(面积和周长)有怎样的关系?四边形ADEF的周长与AB+AC的关系如何?例3、已知在四边形ABCD中,AB=CD,E、F、G分别是BD、AC、BC的中点,H是EF的中点.求证:EF⊥GH.例4、已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.1OFEADCBHGOFEADCBHGOFEADCB书之屋教育二、梯形中位线的性质1、已知等腰梯形的中位线和腰长相等,都等于8cm,这个等腰梯形的周长为()A、16cmB、32cmC、24cmD、40cm2、已知四边形ABCD是高为10的等腰梯形,AB=DC,AD∥BC,又AC⊥BD,求中位线EF的长。3、在梯形ABCD中,AD∥BC,E、F分别是AB、CD的中点,E、F分别交BD、AC于点G、H,求证:GH=(BC-AD).变式一:在梯形ABCD中,AD∥BC,E、F分别是AB、CD的中点,E、F分别交BD、AC于点G、H,AD=a,BC=b,求EF、FH、GH的长。2ABCDEFGHHGOFEADCBEADCBDlACA'C'BD'FBADCEGEBACDF书之屋教育变式二:在梯形ABCD中,AD∥BC,G、H分别是BF、AC的中点,求证:EF是梯形ABCD的中位线。4、在梯形ABCD中,AD∥BC,∠BAD与∠ABC的平分线交于CD中点E.求证:AD+BC=AB.5、直线l过口ABCD的顶点B,AA’⊥l,CC’⊥l,DD’⊥l,试证明AA’+CC’=DD’三、直角三角形和中位线1、在Rt△ABC中,∠BAC=90°,延长BA到D,使AD=AB,E、F分别是BC、AC的中点。(1)求证:DF=BE;(2)过点A作AG∥BC,与DF相交于点G,求证:AG=DG.2、(中线与中位线)已知AD是△ABC的中线,E是AD的中点,求证:FC=2AF.3DGFBACEDMBACADCBFEABC(A)P(E)书之屋教育3、如图,在△ABC中,D、E、F分别为三边中点,AG是BC边上的高,求证:四边形DGEF是等腰梯形。4、已知,如图,AD为△ABC边的高,∠B=2∠C,M为BC的中点.求证:DM=AB5、(方程思想与中位线色综合)在梯形ABCD中,AD∥BC,AB=DC,BD⊥DC,且BD平分∠ABC,若梯形的周长为20,求这个梯形中位线的长。四、中点四边形1、任意四边形的中点四边形都是___________;平行四边形的中点四边形是_____________;矩形的中点四边形是_______________;菱形的中点四边形是__________________;正方形的中点四边形是__________________;梯形的中点四边形是_________________;直角梯形的中点四边形是________________;等腰梯形的中点四边形是______________。五、操作题1、在△ABC中,借助作图工具可以做出中位线EF,沿着中位线EF剪开,用得到的△AEF和四边形EBCF可以拼成口EBCP,剪切线与拼图如图。仿照上述的方法,按要求完成下列操作设计,并画出图示。4书之屋教育(1)在△ABC中,增加条件,沿着剪开后可以拼成矩形,画出剪切线与拼图;(2)在△ABC中,增加条件,沿着剪开后可以拼成菱形,画出剪切线与拼图;(3)在△ABC中,增加条件,沿着剪开后可以拼成正方形,画出剪切线与拼图;(4)在△ABC(ABAC)中,沿着剪切线剪开也可以拼成等腰梯形,首先要确定剪切线,其操作过程(剪切线的做法)是。2、如图,∠BAC=110°,若MP、NQ分别垂直平分AB、AC,则∠PAQ=3、已知:如图,AC⊥OD,AE⊥OF,BD⊥OD,BF⊥OF,AC=AE,求证:BD=BF.4、已知:如图,BP,CP是△ABC的外角平分线,证明:点P一定在∠BAC的角平分线上。5、在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,请说明PB+PC与AB+AC的大小关系并写出证明过程。5QPNMABCABCMNPODBFEACDCABP