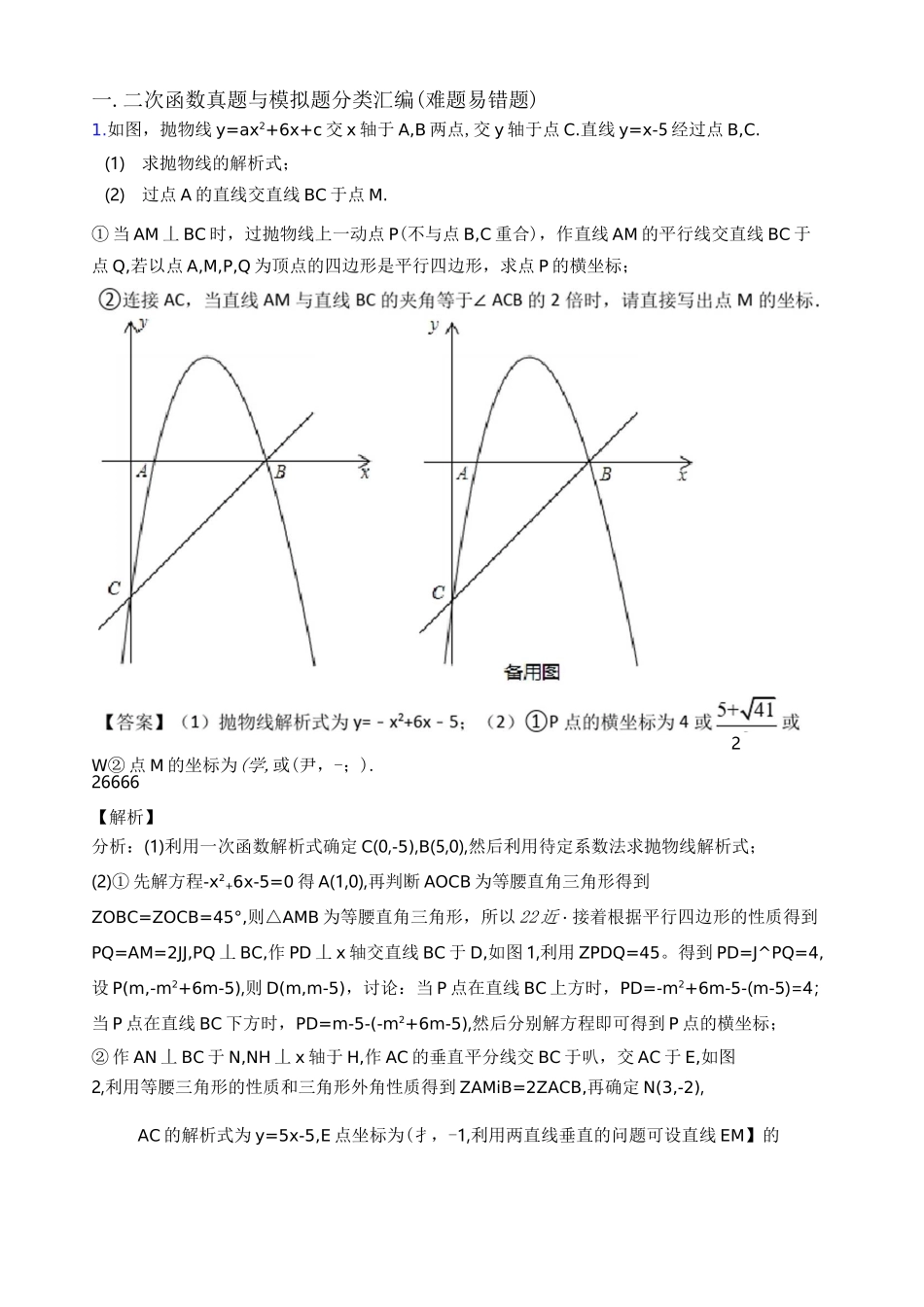
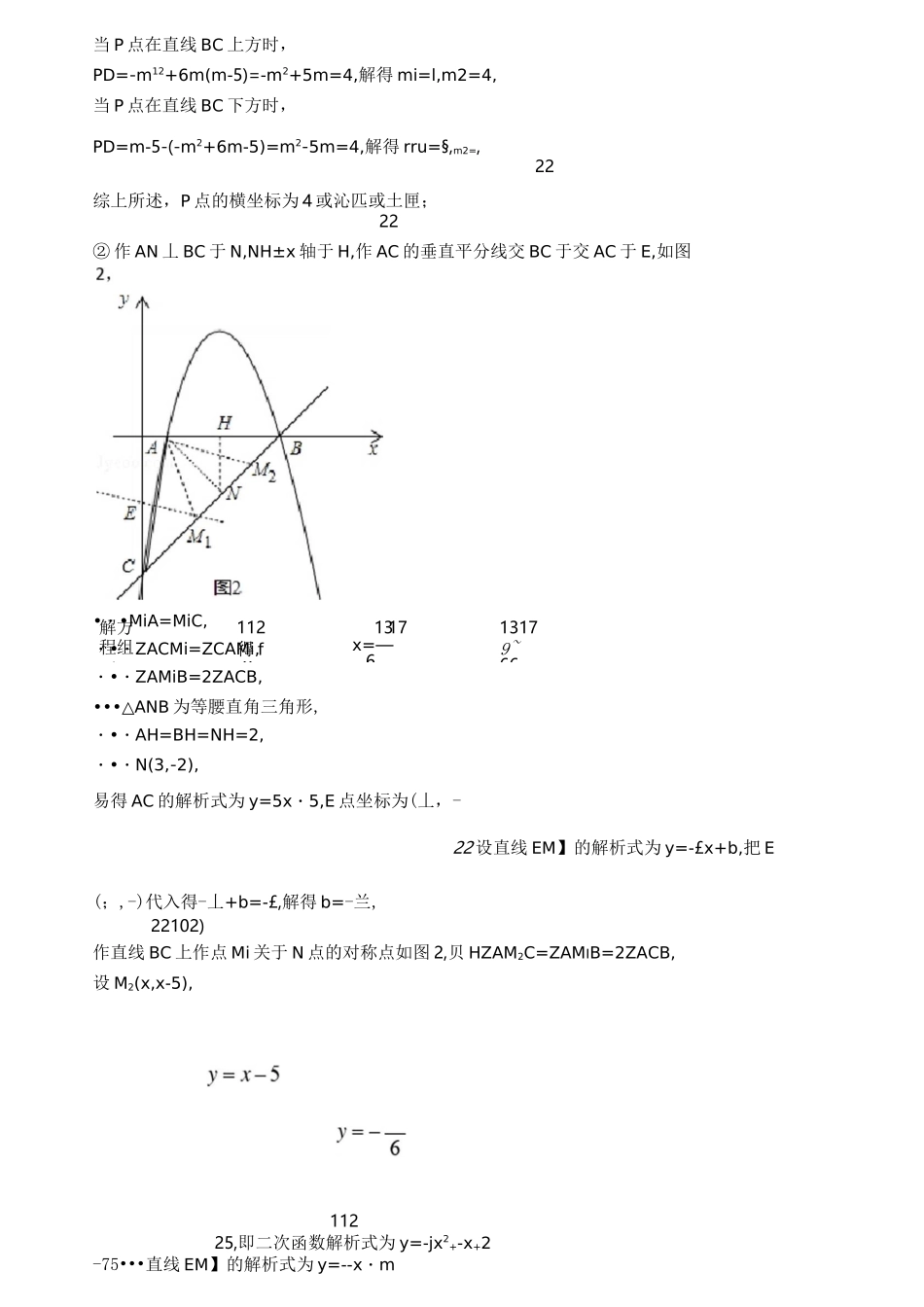
一.二次函数真题与模拟题分类汇编(难题易错题)1.如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x-5经过点B,C.(1)求抛物线的解析式;(2)过点A的直线交直线BC于点M.①当AM丄BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;2W②点M的坐标为(学,或(尹,-;).26666【解析】分析:(1)利用一次函数解析式确定C(0,-5),B(5,0),然后利用待定系数法求抛物线解析式;(2)①先解方程-x2+6x-5=0得A(1,0),再判断AOCB为等腰直角三角形得到ZOBC=ZOCB=45°,则△AMB为等腰直角三角形,所以22近・接着根据平行四边形的性质得到PQ=AM=2JJ,PQ丄BC,作PD丄x轴交直线BC于D,如图1,利用ZPDQ=45。得到PD=J^PQ=4,设P(m,-m2+6m-5),则D(m,m-5),讨论:当P点在直线BC上方时,PD=-m2+6m-5-(m-5)=4;当P点在直线BC下方时,PD=m-5-(-m2+6m-5),然后分别解方程即可得到P点的横坐标;②作AN丄BC于N,NH丄x轴于H,作AC的垂直平分线交BC于叭,交AC于E,如图2,利用等腰三角形的性质和三角形外角性质得到ZAMiB=2ZACB,再确定N(3,-2),AC的解析式为y=5x-5,E点坐标为(扌,-1,利用两直线垂直的问题可设直线EM】的a=-lb=-5解析式为y=--x+b,把E(丄,=)代入求出b得到直线EM】的解析式为尸丄x-楚,则52255fy=—5解方程组彳112得M]点的坐标;作直线BC上作点Ml关于N点的对称点M2,y=——x155如图2,利用对称性得到ZAM2C=ZAMIB=2ZACB,设M2(x,x-5),根据中点坐标公式13.得到3=石七,然后求出x即可得到M2的坐标,从而得到满足条件的点M的坐标.2详解:(1)当x=0时,尸x-5=-5,则C(0,-5),当y=0时,x-5=0,解得x=5,则B(5,0),把B(5,0),C(0,-5)代入y=ax2+6x+c得25d+30+c=0“-,解得<c=••抛物线解析式为Y=-x2+6x-5;(2)①解方程・x2+6x-5=0得xi=l,X2=5,则A(1,0),••B(5,0),C(0,-5),••△OCB为等腰直角三角形,••ZOBC=ZOCB=45°,•・AM丄BC,•-△AMB为等腰直角三角形,•.AM=至AB=亚x4=2J2,22.•以点A,M,P,Q为顶点的四边形是平行四边形,AMIIPQ,•.PQ=AM=272.PQ丄BC,•・・PD=VIPQ=71x2^1=4,设P(m,-m2+6m-5),则D(m,m-5),解方程组<112得f-x13x=—613179~66当P点在直线BC上方时,PD=-m12+6m(m-5)=-m2+5m=4,解得mi=l,m2=4,当P点在直线BC下方时,PD=m-5-(-m2+6m-5)=m2-5m=4,解得rru=§,m2=,22综上所述,P点的横坐标为4或沁匹或土匣;22②作AN丄BC于N,NH±x轴于H,作AC的垂直平分线交BC于交AC于E,如图••・MiA=MiC,•・・ZACMi=ZCAMi,•・・ZAMiB=2ZACB,•••△ANB为等腰直角三角形,•・・AH=BH=NH=2,•・・N(3,-2),易得AC的解析式为y=5x・5,E点坐标为(丄,-22设直线EM】的解析式为y=-£x+b,把E(;,-)代入得-丄+b=-£,解得b=-兰,22102)作直线BC上作点Mi关于N点的对称点如图2,贝HZAM2C=ZAMIB=2ZACB,设M2(x,x-5),11225,即二次函数解析式为y=-jx2+-x+2-75•••直线EM】的解析式为y=--x・m1723・・x=—,6.“237、・・M2(—,-一)661317237综上所述,点M的坐标为(兰,或(三,・—)・6666点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等腰直角的判定与性质和平行四边形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质;会运用分类讨论的思想解决数学问题.2.己知点A(-1,2).B(3,6)在抛物线y=ax2+bx±(1)求抛物线的解析式;⑵如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH、AE,求证:FHIIAE:⑶如图2,直线AB分别交x轴、y轴于C、D两点.点P从点C出发,沿射线CD方向匀速运动,速度为每秒近个单位长度;同时点Q从原点0出发,沿x轴正方向匀速运动,速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.17±、/73【答案】⑴抛物线的解析式为y=x2-x:(2)iiE明见解析;(3)当运动时间为’或615+——£—秒时,QM=2PM・【解析】【分析】(1)(1)A,B的坐标代入抛物线y=ax2+bx中确定解析式;(2)把A点坐标代入所设的AF的解析式,与抛物线的解析式构成方程组,解得G点坐标,再通过证...