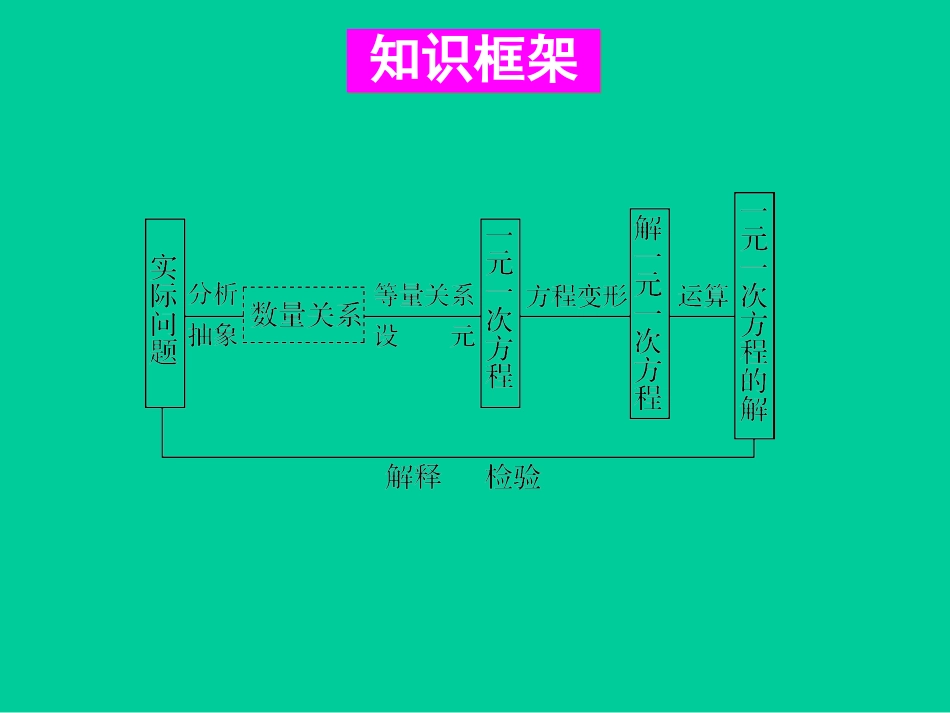
第6章一元一次方程章末复习知识框架知识框架1.方程的解:使方程左右两边的值相等的未知数的值,就是方程的解.2.等式的基本性质:性质1:等式的两边都加上(或减去)同一个数或式子,等式仍然成立.如果a=b,那么a+c=b+c,a-c=b-c.性质2:等式两边都乘或除以同一个数或式子(除数不为0),等式仍然成立.如果a=b,那么ac=bc,a/c=b/c(c≠0).复习巩固复习巩固3.方程的变形方法:方程的两边都加上或(都减去)同一个数或同一个整式,方程的解不变.方程两边都乘以(或都除以)同一个不为零的数,方程的解不变.方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项.4.一元一次方程的概念:只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1的方程叫做一元一次方程.5.解一元一次方程的一般步骤为:去分母,去括号,移项,合并同类项,系数化为1.6.等积类应用题的基本关系式是:变形前的体积=变形后的体积.7.利息的计算方法:利息=本金×利率×期数本息和=本金+利息=本金+本金×利率×期数=本金×(1+利率×期数)8.利润问题中的等量关系式:商品利润=商品售价-商品进价商品售价=商品标价×折扣数商品利润/商品进价×100%=商品利润率商品售价=商品进价×(1+利润率)9.行程问题中基本数量关系是:路程=速度×时间,变形可得到:速度=路程÷时间,时间=路程÷速度.常见题型是相遇问题、追及问题,不管哪个题型都有以下的相等关系:相遇:相遇时间×速度和=路程和,追及:追及时间×速度差=被追及距离.10.工程问题中的等量关系式:工作量=工作效率×工作时间.11.运用方程解实际问题的一般过程:(1)审题:分析题意,找出题中的各个量及其关系;(2)设元:选择一个适当的未知数用字母表示;(3)列方程:根据相等关系列出方程;(4)解方程:求出未知数的值;(5)检验:检验求出的值是否正确或符合实际情形;(6)答:写出答案.典例分析典例分析例1方程y-10=-4y的解是()A.y=1B.y=2C.y=3D.y=4B例2给出下面四个方程及变形:(1)4x+10=0,变形为2x+5=0;(2)x+7=5-3x,变形为4x=12;(3)2/3x=5,变形为2x=15;(4)16x=-8,变形为x=-2;其中方程变形正确的编号组为()A.(1)(2)B.(1)(2)(3)(4)C.(1)(3)D.(1)(2)(3)C例3解方程5x-7+3x=6x+1.解:5x+3x-6x=1+72x=8x=4例4某企业对应聘人员进行英语考试,试题由50道选择题组成,评分标准规定:每道题的答案选对得3分,不选得0分,选错倒扣1分,已知某人有5道题未做,得了103分,则这个人选错了多少题?分析:等量关系是:选对所得的分-选错所扣的分=最后的得分解:设这人选错了x道题,则选对了(50-5-x)道.3(50-5-x)-x=103解这个方程得x=8.答:这个人选错了8道题.例5某校学生进行军训,以每小时5千米的速度去执行任务,出发4小时12分钟后,学校军训指挥部派通讯员骑摩托车追赶学生队伍传达新任务,用了36分钟赶上了队伍,求摩托车的速度分析:等量关系是:学生队伍的行进路程=摩托车行驶的路程.解:设摩托车的速度为每小时x千米.根据题意,列方程得:解这个方程得x=40.答:摩托车的速度为每小时40千米.1.若关于x的方程3(x-1)+a=b(x+1)(a,b为常数)是一元一次方程,则()A.a,b为任意有理数B.a≠0C.b≠0D.b≠3巩固提高巩固提高D2.方程|2x-1|=4x+5的解是()A.x=-3或x=-2/3B.x=3或x=2/3C.x=-2/3D.x=-3C3.解方程3/4×(4/3x-1)=3,下列变形中,较简捷的是()A.方程两边都乘以4,得3(4/3x-1)=12B.去括号,得x-3/4=3C.两边同除以3/4,得4/3x-1=4D.整理,得(4x-3)/4=3B4.解方程(1)5(x-4)-7(7-x)-9=12-3(9-x)解:5x-20-49+7x-9=12-27+3x5x-3x+7x=12-27+20+49+99x=63x=7(2)x-2[x-3(x-1)]=8解:x-2[x-3x+3]=8x-2x+6x-6=8x-2x+6x=8+65x=14x=2.85.某校组织学生春游,如果包租相同的大巴3辆,那么就有14人没有座位;如果多包租1辆,那么就多了26个空位,问春游的总人数是多少?分析:本题若直接设总人数则较难列出方程,所以可以改设每辆大巴的座位数为x较方便.等量关系为:两种方案中的总人数相同.解:设每辆大巴的座位数为x人,根据题意列方程得3x+14=4x-26解这个方程得x=40所以...