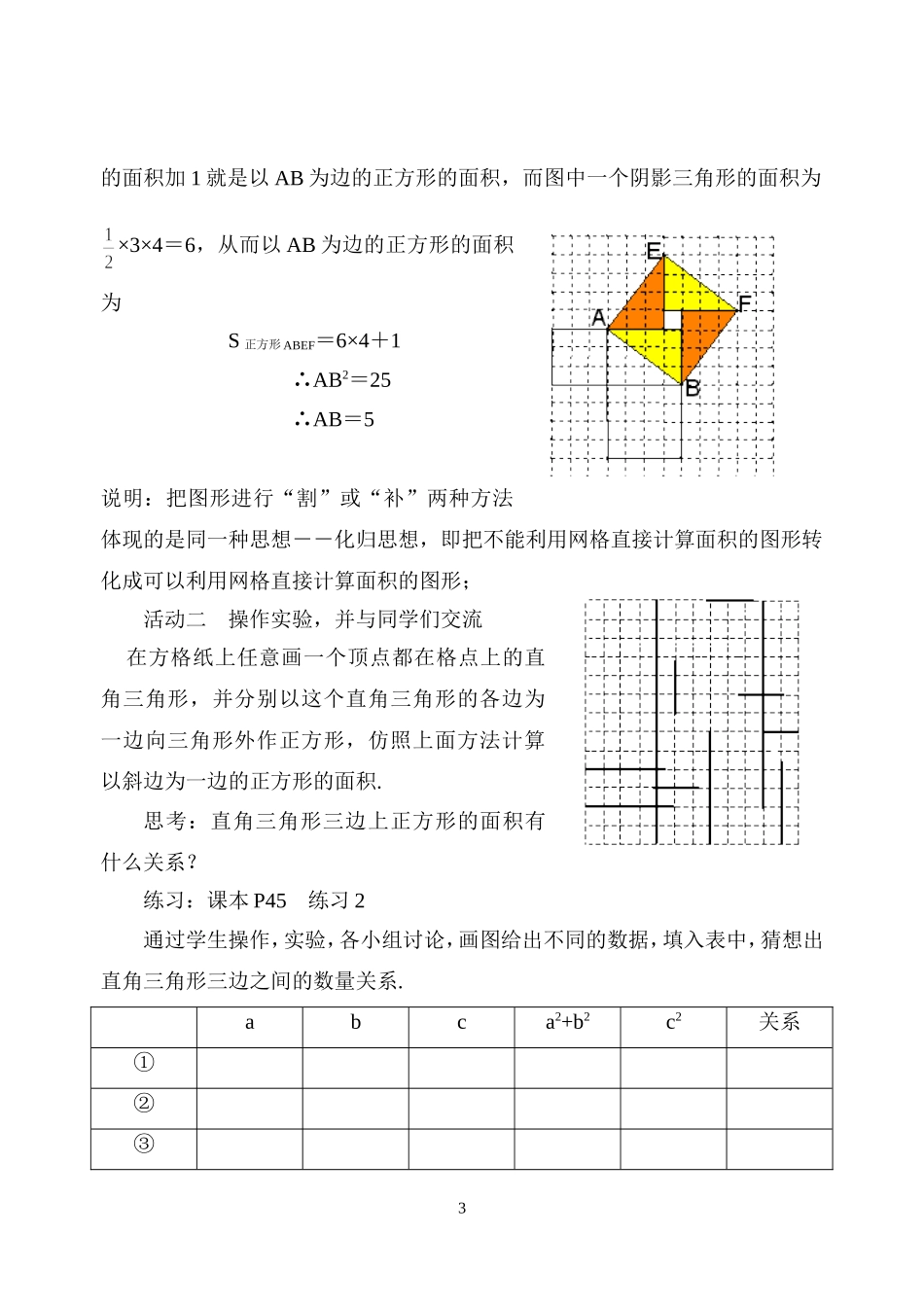
第二章勾股定理与平方根第1课时编写:徐坚审定:陆海泉课题:勾股定理(1)教学目标:1、能说出勾股定理的内容,并能用勾股定理进行简单的计算.2、让学生经历探索勾股定理的过程,发展合情推理的能力,体会数形结合的思想.重点:勾股定理及其应用难点:利用图形的割补验证勾股定理教学过程:一、学情检查1、情境创设这是1955年希腊发行的一枚纪念邮票,观察这枚邮票图案小方格的个数,你有哪些发现?(课本P44)二、合作交流1、探索活动活动一如图12×12的网格上,每一小格的面积为1,以BC为一边的正方形的面积是9,以AC为一边的正方形的面积是16,思考:(1)猜想图中以AB为边的正方形面积是多少?说说你是如何想的?(2)你能说明你的猜想是正确的吗?(3)你能解释书中P44,把图形进行“割”或“补”计算的过程吗?解法一:把以AB为边的正方形放在7×7的网格纸上,我们会看到以AB为边的正方形的面积等于7×7的正方形减去4个三角形ABC的面积,如图所示:S正方形ABEF=×3×4×4=25∴AB2=25∴AB=5解法二:如图把AB为边的正方形分割成下图所示的情况,四个直角三角形2的面积加1就是以AB为边的正方形的面积,而图中一个阴影三角形的面积为×3×4=6,从而以AB为边的正方形的面积为S正方形ABEF=6×4+1∴AB2=25∴AB=5说明:把图形进行“割”或“补”两种方法体现的是同一种思想--化归思想,即把不能利用网格直接计算面积的图形转化成可以利用网格直接计算面积的图形;活动二操作实验,并与同学们交流在方格纸上任意画一个顶点都在格点上的直角三角形,并分别以这个直角三角形的各边为一边向三角形外作正方形,仿照上面方法计算以斜边为一边的正方形的面积.思考:直角三角形三边上正方形的面积有什么关系?练习:课本P45练习2通过学生操作,实验,各小组讨论,画图给出不同的数据,填入表中,猜想出直角三角形三边之间的数量关系.abca2+b2c2关系①②③3④得出结论:勾股定理:直角三角形两直角边的平方和等于斜边的平方.剖析:(1)这是直角三角形的重要性质,揭示了直角三角形的三边之间的重要数量关系(2)体现了一个重要的数学思想:数形结合,即只要知道“形”—直角三角形,即可得到“数”—直角边的平方和等于斜边的平方.(数量关系)(3)符号语言:在Rt△ABC中,若∠C=90°,则a2+b2=c2(4)Rt△ABC中,已知任意两边可求第三边(5)用面积关系解释勾股定理简介勾股定理的历史资料,见书P45例1、在Rt△ABC中,∠C=90°(1)已知a=6,c=10,求b;(1)已知a=40,b=9,求c;(3)已知c=25,b=15,求a.练习:课本P451、2例2如图△ABC中,∠ACB=90°,AB=50cm,BC=30cm,CD⊥AB于D,求CD的长.解: ∠ACB=90°,AB=50cm,BC=30cm,∴AC2=AB2-BC2=2500-900=1600=402∴AC=40cm又 S△ABC=BC·AC=AB·CD∴BC·AC=AB·CD∴CD==24cm4答:CD的长24cm.小结:本题需要认真审题,否则容易掉下“陷阱”去想利用勾股定理来求CD的长,暂时很难求,我们应从条件出发逐步进行分析,可以先求AC=40cm,下面只能用面积公式来求CD,这一知识点也非常重要,而且在几何的计算和证明中会经常用到,要认真巩固.例3、一棵树在台风“卡努”的袭击下,在离地5米断裂,树顶落在离根12米远处,问这棵树断之前有多高?三、总结反思1、勾股定理“直角三角形两直角边的平方和等于斜边的平方”是直角三角形的又一条重要性质;2、勾股定理揭示了“形”与“数”的内在联系,是数形结合的经典一例.四、分层训练1、在Rt△ABC中,∠C=90°(1)如果BC=9,AC=12,则AB=___(2)如果BC=40,AC=41,则AB=___2、如图,△AD⊥BC于D,AB=3,BD=2,DC=1,求AC53、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为_______cm2.★4、(1)在Rt△ABC中,∠C=90,周长为60,斜边与一条直角边之比为13∶5,则这个三角形三边长分别是()A、5、4、3、;B、13、12、5;C、10、8、6;D、26、24、10★★5、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是()A、20cm;B、10cm;C...