高三数学 名校尖子生培优专题系列 填空题训练3 图象解析法教案 新人教A版-新人教A版高三全册数学教案VIP免费

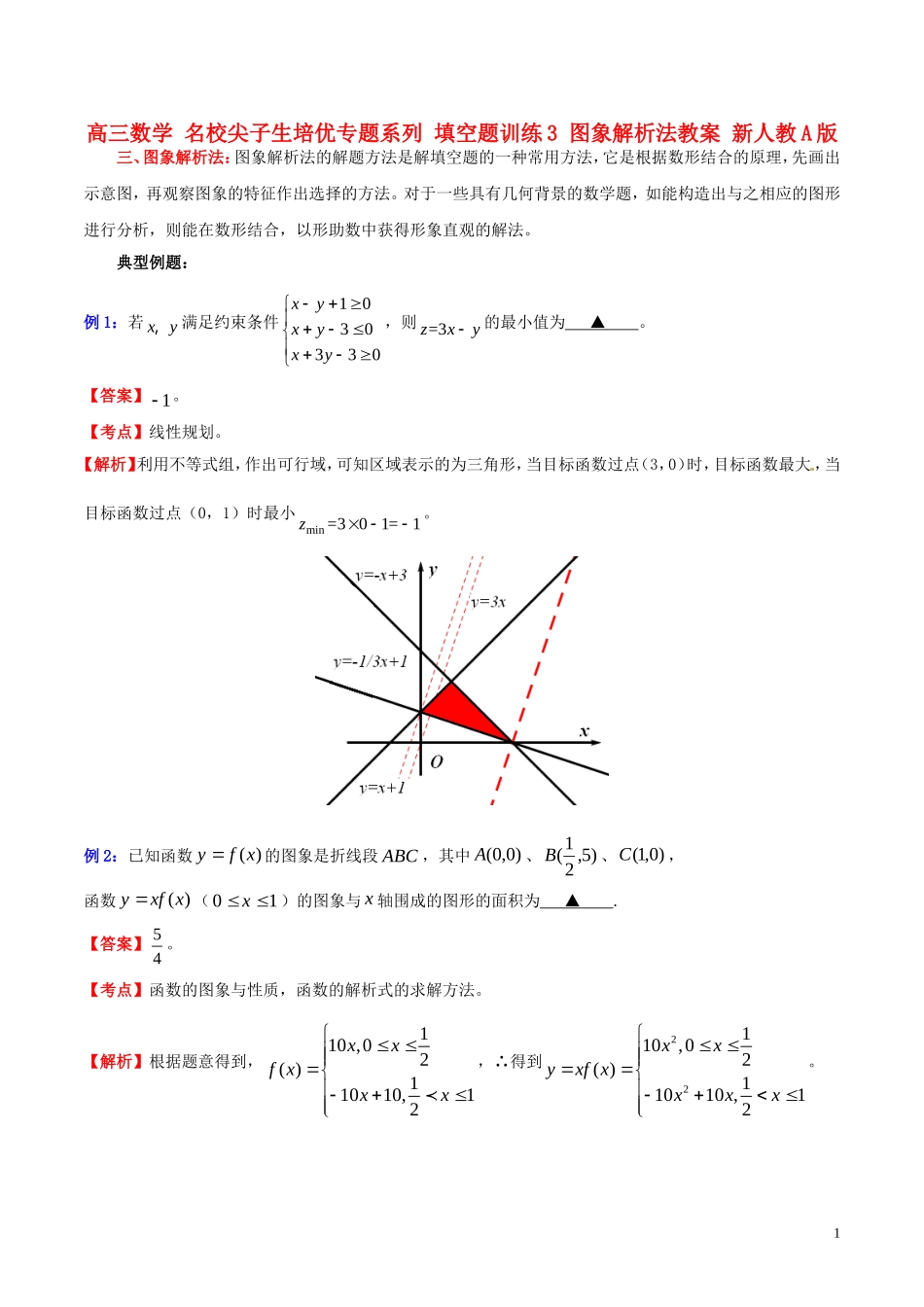
高三数学名校尖子生培优专题系列填空题训练3图象解析法教案新人教A版三、图象解析法：图象解析法的解题方法是解填空题的一种常用方法，它是根据数形结合的原理，先画出示意图，再观察图象的特征作出选择的方法。对于一些具有几何背景的数学题，如能构造出与之相应的图形进行分析，则能在数形结合，以形助数中获得形象直观的解法。典型例题：例1：若xy，满足约束条件1030330xyxyxy，则=3zxy的最小值为▲。【答案】1。【考点】线性规划。【解析】利用不等式组，作出可行域，可知区域表示的为三角形，当目标函数过点（3，0）时，目标函数最大，当目标函数过点（0，1）时最小min=301=1z。例2：已知函数)(xfy的图象是折线段ABC，其中)0,0(A、)5,21(B、)0,1(C，函数)(xxfy（10x）的图象与x轴围成的图形的面积为▲.【答案】54。【考点】函数的图象与性质，函数的解析式的求解方法。【解析】根据题意得到，110,02()11010,12xxfxxx，∴得到22110,02()11010,12xxyxfxxxx。1)(xfy的图象如图1，)(xxfy（10x）的图象如图2。易知，)(xxfy（10x）的分段解析式中的两部分抛物线形状完全相同，只是开口方向及顶点位置不同，，封闭图形MNO与OMP全等，面积相等，故所求面积即为矩形ODMP的面积155224S。若用定积分求解，则1122220151010104xdxxxdx。例3：已知函数2|1|=1xyx的图象与函数=2ykx的图象恰有两个交点，则实数k的取值范围是▲.【答案】(0,1)(1,4)。【考点】函数的图像及其性质，利用函数图像确定两函数的交点。【分析】函数1)1)(1(112xxxxxy，当1x时，11112xxxxy，当1x时，1,111,11112xxxxxxxy，综上函数1,111,111112xxxxxxxxy，。作出函数的图象，要使函数y与kxy有两个不同的交点，则直线kxy必须在蓝色或黄色区域2内，如图，此时当直线经过黄色区域时)2,1(B，k满足21k，当经过蓝色区域时，k满足10k，综上实数k的取值范围是(0,1)(1,4)。例4：）对于实数a和b，定义运算“*”：a*b＝设(21)*(1)fxxx，且关于x的方程()fxmmR恰有三个互不相等的实数根x1，x2，x3，则x1x2x3的取值范围是▲．【答案】。【考点】新定义，分段函数的图象和性质，分类讨论和数形结合思想的应用。【解析】根据新运算符号得到函数为22(21)(21)(1)(21)(1)(21)*(1)=(1)(21)(1)(21)(1)xxxxxfxxxxxxx>x，，，化简得：2220=+0xxxfxxxx>，，。如图，作出函数2220=+0xxxfxxxx>，，和ym的图象，如果fxm有三个不同的实数解，即直线ym与函数f(x)的图象有三个交点，如图，（1）当直线ym过抛物线2+yxx的顶点1124，或=0ym时，有两个交点；（2）当直线ym中104m>m<时，有一个交点；（3）当直线ym中104y>，，求yx的取值范围。作出（xy，）所在平面区域（如图）。求出=xye的切线的斜率e，设过切点00Pxy，的切线为=0yexmm，则00000==yexmmexxx，要使它最小，须=0m。∴yx的最小值在00Pxy，处，为e。此时，点00Pxy，在=xye上,AB之间。当（xy，）对应点C时，=45=205=7=7=534=2012yxyxyyxyxyxx，∴yx的最大值在C处，为7。∴yx的取值范围为7e，，即ba的取值范围是7e，。4