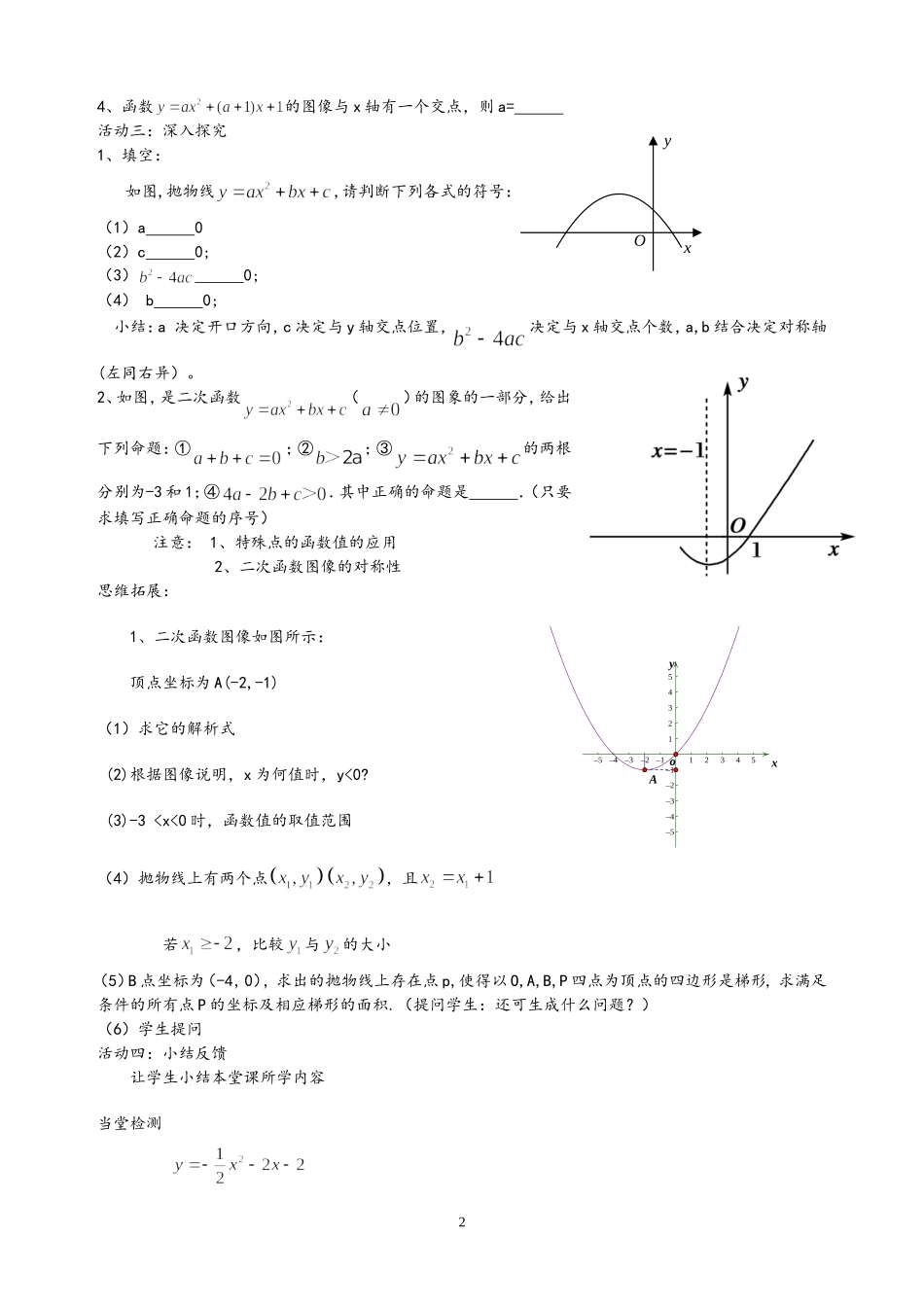
二次函数复习(1)南通市虹桥二中刘勇教材分析:二次函数在初中函数的教学中有重要地位,它不仅是初中代数内容的引申,更为高中学习一元二次不等式和圆锥曲线奠定基础。在历届中考试题中,二次函数都是综合题中不可缺少的内容。二次函数的图像和性质体现了数形结合的数学思想,对学生基本数学思想和素养的形成起推动作用。教学目的:1、深化对二次函数的图像及其性质的理解、并能灵活运用二次函数及其图像的性质解决有关问题。2、培养学生良好的逻辑思维及说理能力。教学重点:二次函数的图像及性质的运用。教学方法:师生互动探究式教学以教学大纲为依据,渗透新的教育理念,遵循师生协同的原则,结合初三学生的求知心理和已有的认知水平开展教学.形成学生自动、生生助动、师生互动,教师着眼于引导,学生着眼于探索,侧重于学生能力的提高、思维的训练。教学过程:活动一:请根据所给的函数写出相关结论.比一比赛一赛看谁写的多?设计意图:由提问引入本课复习的主要复习知识点:二次函数的定义,三种表达方式,图像的基本性质。活动二:知识梳理二次函数()y=a(x-h)2+ky=ax2+bx+c开口方向对称轴顶点坐标最值增减性基础训练:1、函数,当m=时,它是二次函数2、抛物线上有两个点,若,则与的大小关系是3、抛物线的对称轴是,顶点坐标是当x=时,y有最值,此值是。122(1)1yxxy12345–1–2–3–4–512345–1–2–3–4–5Ao4、函数的图像与x轴有一个交点,则a=活动三:深入探究1、填空:如图,抛物线,请判断下列各式的符号:(1)a0(2)c0;(3)0;(4)b0;小结:a决定开口方向,c决定与y轴交点位置,决定与x轴交点个数,a,b结合决定对称轴(左同右异)。2、如图,是二次函数()的图象的一部分,给出下列命题:①;②;③的两根分别为-3和1;④.其中正确的命题是.(只要求填写正确命题的序号)注意:1、特殊点的函数值的应用2、二次函数图像的对称性思维拓展:1、二次函数图像如图所示:顶点坐标为A(-2,-1)(1)求它的解析式(2)根据图像说明,x为何值时,y<0?(3)-3