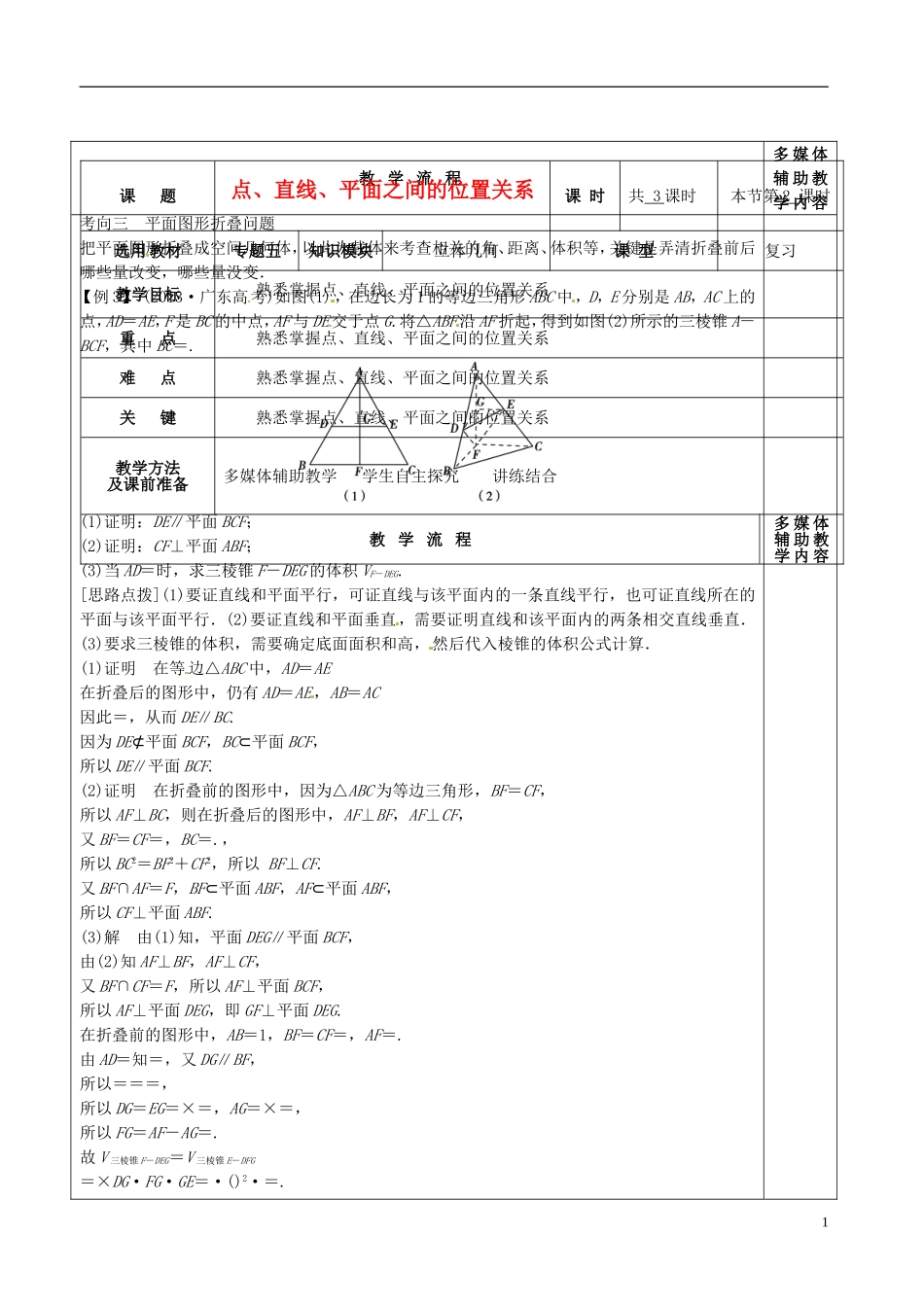
教学流程多媒体辅助教学内容考向三平面图形折叠问题把平面图形折叠成空间几何体,以此为载体来考查相关的角、距离、体积等,关键是弄清折叠前后哪些量改变,哪些量没变.【例3】(2013·广东高考)如图(1),在边长为1的等边三角形ABC中,D,E分别是AB,AC上的点,AD=AE,F是BC的中点,AF与DE交于点G.将△ABF沿AF折起,得到如图(2)所示的三棱锥A-BCF,其中BC=.(1)证明:DE∥平面BCF;(2)证明:CF⊥平面ABF;(3)当AD=时,求三棱锥F-DEG的体积VF-DEG.[思路点拨](1)要证直线和平面平行,可证直线与该平面内的一条直线平行,也可证直线所在的平面与该平面平行.(2)要证直线和平面垂直,需要证明直线和该平面内的两条相交直线垂直.(3)要求三棱锥的体积,需要确定底面面积和高,然后代入棱锥的体积公式计算.(1)证明在等边△ABC中,AD=AE在折叠后的图形中,仍有AD=AE,AB=AC因此=,从而DE∥BC.因为DE⊄平面BCF,BC⊂平面BCF,所以DE∥平面BCF.(2)证明在折叠前的图形中,因为△ABC为等边三角形,BF=CF,所以AF⊥BC,则在折叠后的图形中,AF⊥BF,AF⊥CF,又BF=CF=,BC=.,所以BC2=BF2+CF2,所以BF⊥CF.又BF∩AF=F,BF⊂平面ABF,AF⊂平面ABF,所以CF⊥平面ABF.(3)解由(1)知,平面DEG∥平面BCF,由(2)知AF⊥BF,AF⊥CF,又BF∩CF=F,所以AF⊥平面BCF,所以AF⊥平面DEG,即GF⊥平面DEG.在折叠前的图形中,AB=1,BF=CF=,AF=.由AD=知=,又DG∥BF,所以===,所以DG=EG=×=,AG=×=,所以FG=AF-AG=.故V三棱锥F-DEG=V三棱锥E-DFG=×DG·FG·GE=·()2·=.课题点、直线、平面之间的位置关系课时共3课时本节第2课时选用教材专题五知识模块立体几何课型复习教学目标熟悉掌握点、直线、平面之间的位置关系重点熟悉掌握点、直线、平面之间的位置关系难点熟悉掌握点、直线、平面之间的位置关系关键熟悉掌握点、直线、平面之间的位置关系教学方法及课前准备多媒体辅助教学学生自主探究讲练结合教学流程多媒体辅助教学内容1[探究提升]1.解决与翻折有关的几何问题的关键是搞清翻折前后哪些量改变,哪些量不变,抓住翻折前后不变的量,充分利用原平面图形的信息进行条件转化.2.求解过程中,要综合考虑折叠前后的图形,把平面图形翻折后,经过恰当连线就能得到三棱锥、四棱锥,从而把问题转化到我们熟悉的几何体中去解决.【变式训练3】如图所示,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合于点G,得到多面体CDEFG.(1)求证:平面DEG⊥平面CFG;(2)求多面体CDEFG的体积.(1)证明 CD∥EF,且DE⊥EF,CF⊥EF.∴四边形CDEF为矩形. GD=AD=5,DE=4,∴GE==3.由GC=BC=4,CF=4,得FG==4,所以EF=5.在△EFG中,有EF2=GE2+FG2,所以EG⊥GF.又因为CF⊥EF,CF⊥FG,所以CF⊥平面EFG.所以CF⊥EG,所以EG⊥平面CFG.又EG⊂平面DEG,所以平面DEG⊥平面CFG.(2)解如图,在平面EGF中,过点G作GH⊥EF于点H,则GH==.因为平面CDEF⊥平面EFG,所以GH⊥平面CDEF,所以V多面体CDEFG=S矩形CDEF·GH=16.课堂同步练习:1.(2013·浙江高考)设m,n是两条不同的直线,α,β是两个不同的平面().A.若m∥α,n∥α,则m∥nB.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β解析平行的传递性只有在线线和面面之间,则A,B不正确.两条平行线中,有一条直线垂直于一个平面,那么另一条直线也垂直这个平面,C正确.考点探究突破典型例题讲解,先让学生自己思考,老师再给出思2答案C2.(2013·北京高考)如图,在正方体ABCDA1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有().A.3个B.4个C.5个D.6个解析设正方体边长为1,过P作平面A1B1C1D1,ABCD的垂线分别交D1B1,DB于E,F点,易知P也是EF的三等分点,则PA=PC=PB1=,PA1=PD=PC1=1,PB=,PD1=共有4个.答案B3.(2013·广东高考)设l为直线,α,β是两个不同的平面,下列命题中正确的是().A.若l∥α,l∥β,则α∥βB.若l⊥α,l⊥β,则α∥βC.若l⊥α...