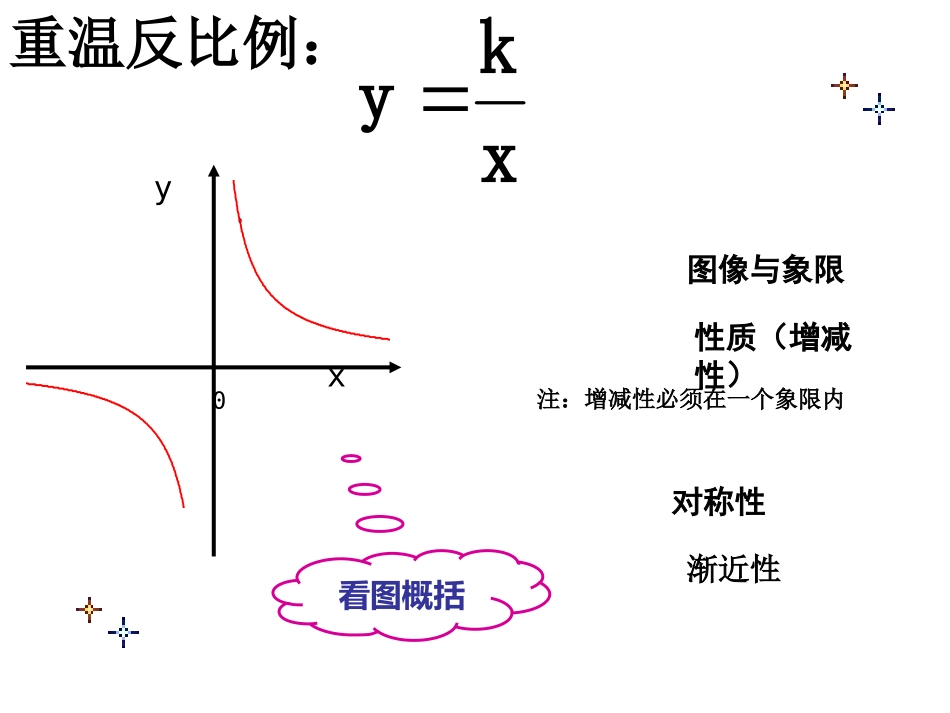
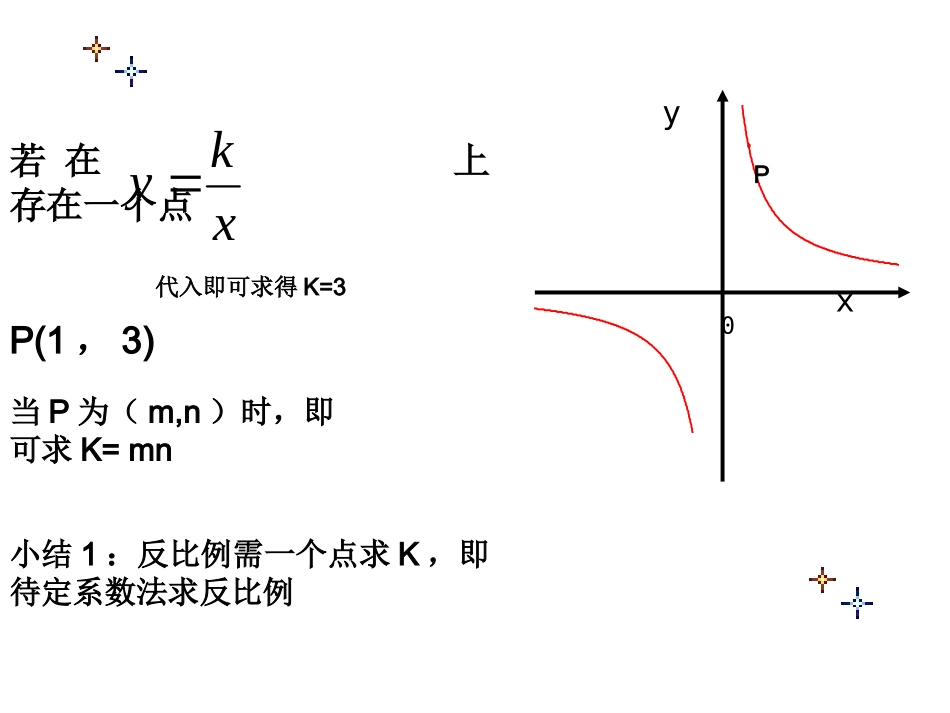
xy0xy0乐清市天成第一中学数学组叶慧飞y0x图像与象限性质(增减性)对称性注:增减性必须在一个象限内看图概括重温反比例:xky渐近性y0xP小结1:反比例需一个点求K,即待定系数法求反比例代入即可求得K=3若在上存在一个点P(1,3)xky当P为(m,n)时,即可求K=mn延伸1:P(m,n)oyx||||||knmAPOASOAPB反比例的面积不变性mn过P(m,n)作X轴或Y轴交点A与OP成三角形,有什么收获?AB练习1:点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为1.5,则这个反比例函数的关系式是.xyoMNpx3y延伸2:Pyxoy1=x-2过P作一次函数y=x-2和反比例函数交于P、B两点_3xy=BC同学们,看右图,你有什么收获?(1)求P、B两点的坐标。(2)x取何值时,y1y﹥2。(1)注:求公共点即求它们的二元方程组应用:小结2:一次函数把反比例分截成四段,即截图法Pyxoy1=x-23-1BCPBCyxoy1=x-2_3xy2=连结PO和OB,求的面积OPBS注:求面积时,一般把图形分割以X轴或Y轴平行线为底展开知识延伸3:小结3:反比例与一次函数的应用关键在于它们公共交点的处理1.下列式子中,表示y是x的反比例函数的是()A.B.C.D.21xy3xy1xy1xxy2.若是反比例函数,则m的值是()A.m=3B.m=4C.m=1或m=4D.m=2或m=3552)2(mmxmyCA3.已知点A(-2,y1),B(-1,y2)都在反比例函数的图象上,则y1、y2与y3的大小关系(从大到小)为.x4yA(-2,y1),B(-1,y2),C(4,y3)yxo-1y1y2AB-24Cy3y3>y1>y2如图,已知反比例函数y=的图象与一次函数y=kx+4的图象相交于P、Q两点,且P点的纵坐标是6,且直线y=kx+4与坐标轴交于A、B两点。(1)求这个一次函数的解析式(2)求△POQ的面积xoPQ12xM∟N∟(x,6)6(2,6)(1)y=x+4(-4,0)4(-6,-2)2(2)SPQO△=SAQO△+SAOP△yAB