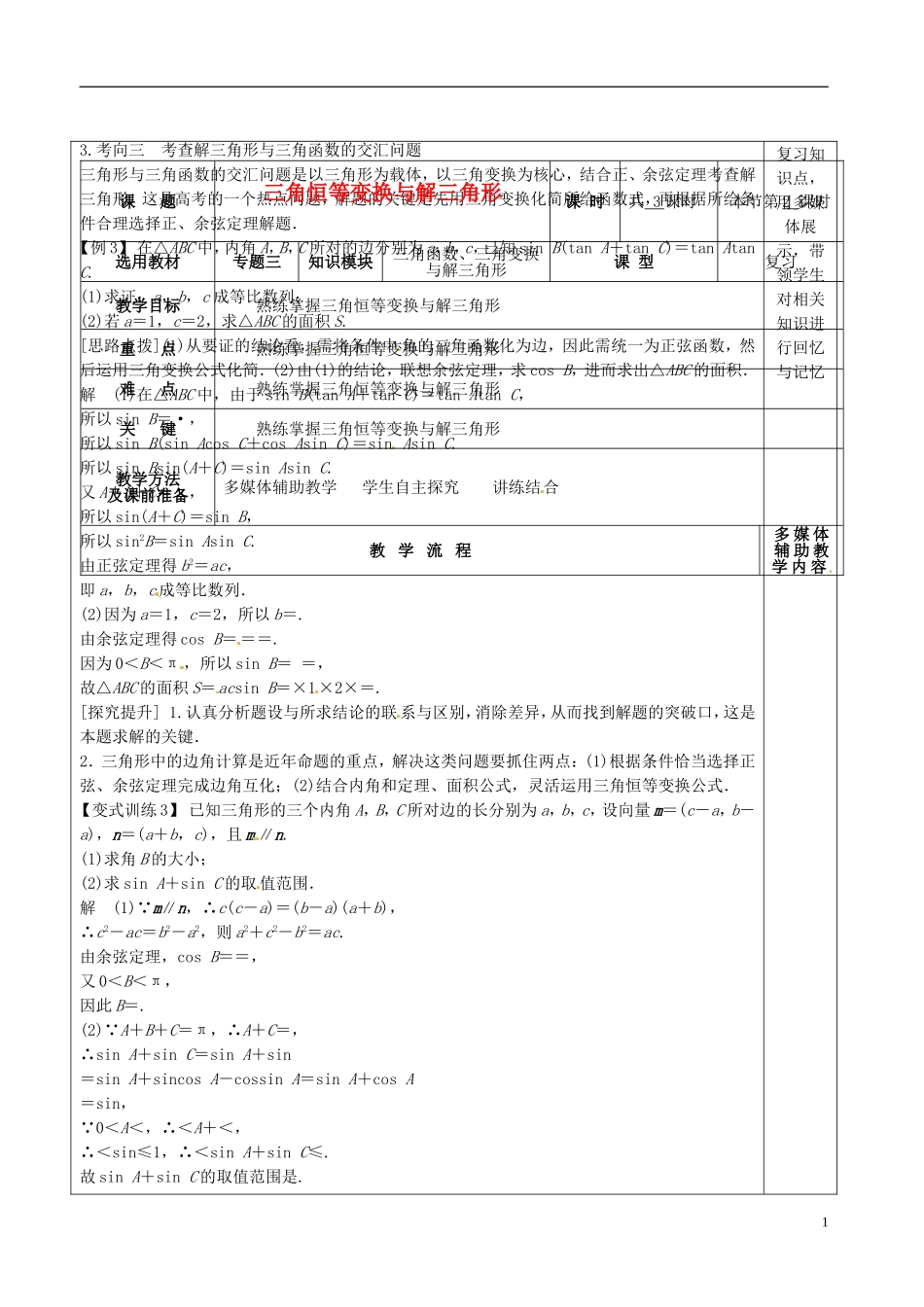
3.考向三考查解三角形与三角函数的交汇问题三角形与三角函数的交汇问题是以三角形为载体,以三角变换为核心,结合正、余弦定理考查解三角形,这是高考的一个热点问题,解题的关键是先用三角变换化简所给函数式,再根据所给条件合理选择正、余弦定理解题.【例3】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB(tanA+tanC)=tanAtanC.(1)求证:a,b,c成等比数列;(2)若a=1,c=2,求△ABC的面积S.[思路点拨](1)从要证的结论看,需将条件中角的三角函数化为边,因此需统一为正弦函数,然后运用三角变换公式化简.(2)由(1)的结论,联想余弦定理,求cosB,进而求出△ABC的面积.解(1)在△ABC中,由于sinB(tanA+tanC)=tanAtanC,所以sinB=·,所以sinB(sinAcosC+cosAsinC)=sinAsinC.所以sinBsin(A+C)=sinAsinC.又A+B+C=π,所以sin(A+C)=sinB,所以sin2B=sinAsinC.由正弦定理得b2=ac,即a,b,c成等比数列.(2)因为a=1,c=2,所以b=.由余弦定理得cosB===.因为0<B<π,所以sinB==,故△ABC的面积S=acsinB=×1×2×=.[探究提升]1.认真分析题设与所求结论的联系与区别,消除差异,从而找到解题的突破口,这是本题求解的关键.2.三角形中的边角计算是近年命题的重点,解决这类问题要抓住两点:(1)根据条件恰当选择正弦、余弦定理完成边角互化;(2)结合内角和定理、面积公式,灵活运用三角恒等变换公式.【变式训练3】已知三角形的三个内角A,B,C所对边的长分别为a,b,c,设向量m=(c-a,b-a),n=(a+b,c),且m∥n.(1)求角B的大小;(2)求sinA+sinC的取值范围.解(1) m∥n,∴c(c-a)=(b-a)(a+b),∴c2-ac=b2-a2,则a2+c2-b2=ac.由余弦定理,cosB==,又0<B<π,因此B=.(2) A+B+C=π,∴A+C=,∴sinA+sinC=sinA+sin=sinA+sincosA-cossinA=sinA+cosA=sin, 0<A<,∴<A+<,∴<sin≤1,∴<sinA+sinC≤.故sinA+sinC的取值范围是.复习知识点,用多媒体展示,带领学生对相关知识进行回忆与记忆课题三角恒等变换与解三角形课时共3课时本节第2课时选用教材专题三知识模块三角函数、三角变换与解三角形课型复习教学目标熟练掌握三角恒等变换与解三角形重点熟练掌握三角恒等变换与解三角形难点熟练掌握三角恒等变换与解三角形关键熟练掌握三角恒等变换与解三角形教学方法及课前准备多媒体辅助教学学生自主探究讲练结合教学流程多媒体辅助教学内容1考向四正(余)弦定理的实际应用由于正、余弦定理是解斜三角形的工具,测量、航海问题是高考的热点.求解这类问题的关键是由题意构建三角形模型,借助正弦、余弦定理求解.【例4】如图所示,A,B是海面上位于东西方向相距5(3+)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20海里的C点的救援船立即前往营救,其航行速度为30海里/时,该救援船到达D点需要多长时间?[思路点拨]由题设条件,要求救援船到达D点的时间只需求CD的长,先在△ABD中求BD,再在△BDC中求CD,进而求出时间.解由题意知AB=5(3+)海里,∠DBA=90°-60°=30°,∠DAB=45°,∴∠ADB=105°.∴sin105°=sin45°·cos60°+cos45°·sin60°=×+×=.在△ABD中,由正弦定理得:=,∴BD=====10(海里).又∠DBC=180°-60°-60°=60°,BC=20海里,在△DBC中,由余弦定理得CD2=BD2+BC2-2·BD·BC·cos60°=300+1200-2×10×20×=900.∴CD=30(海里),∴救援船需要的时间t==1(小时).即救援船到达D点需要1小时.[探究提升]应用解三角形知识解决实际问题需要下列三步:(1)根据题意,画出示意图,并标出条件.(2)将所求问题归结到一个或几个三角形中,通过合理运用正、余弦定理等有关知识正确求解.(3)检验解出的结果是否符合实际意义,得出正确答案.【变式训练4】如图,A,C两岛之间有一片暗礁,一艘小船于某日上午8时从A岛出发,以10海里/时的速度沿北偏东75°方向直线航行,下午1时到达B处.然后以同样的速度沿北偏东15°方向直线航行,下午4时到达C岛.(1)求A,C两岛之间的距离;(2)求∠BAC的正弦值...